Electrostatics 3 Question 13
13. An infinitely long thin non-conducting wire is parallel to the $Z$-axis and carries a uniform line charge density $\lambda$. It pierces a thin non-conducting spherical shell of radius $R$ in such a way that the $\operatorname{arc} P Q$ subtends an angle $120^{\circ}$ at the centre $O$ of the spherical shell, as shown in the figure. The permittivity of free space is $\varepsilon_{0}$. Which of the following statements is (are) true? (2018 Adv.)
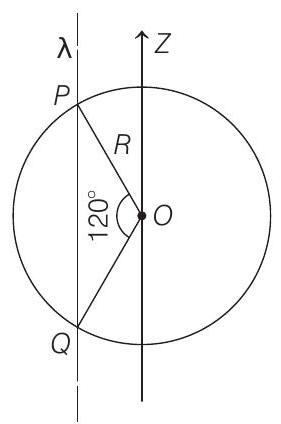
(a) The electric flux through the shell is $\sqrt{3} R \lambda / \varepsilon_{0}$
(b) The $z$-component of the electric field is zero at all the points on the surface of the shell
(c) The electric flux through the shell is $\sqrt{2} R \lambda / \varepsilon_{0}$
(d) The electric field is normal to the surface of the shell at all points
Show Answer
Answer:
Correct Answer: 13. (a,b)
Solution:
- $P Q=(2) R \sin 60^{\circ}$
$ \begin{aligned} & =(2 R) \frac{\sqrt{3}}{2}=(\sqrt{3} R) \\ q_{\text {enclosed }} & =\lambda(\sqrt{3} R) \\ \text { We have, } \quad \varphi & =\frac{q_{\text {enclosed }}}{\varepsilon_{0}} \\ \Rightarrow \quad \varphi & =\frac{\sqrt{3} \lambda R}{\varepsilon_{0}} \end{aligned} $
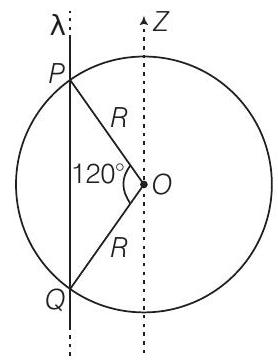
Also, electric field is perpendicular to wire, so $Z$-component will be zero.
