Electrostatics 2 Question 7
7. A charge $Q$ is distributed over three concentric spherical shells of radii $a, b, c(a<b<c)$ such that their surface charge densities are equal to one another.
The total potential at a point at distance $r$ from their common centre, where $r<a$ would be
(Main 2019, 10 Jan I)
(a) $\frac{Q\left(a^{2}+b^{2}+c^{2}\right)}{4 \pi \varepsilon_{0}\left(a^{3}+b^{3}+c^{3}\right)}$
(b) $\frac{Q(a+b+c)}{4 \pi \varepsilon_{0}\left(a^{2}+b^{2}+c^{2}\right)}$
(c) $\frac{Q}{4 \pi \varepsilon_{0}(a+b+c)}$
(d) $\frac{Q}{12 \pi \varepsilon_{0}} \cdot \frac{a b+b c+c a}{a b c}$
Show Answer
Answer:
Correct Answer: 7. (b)
Solution:
- Given charge distribution is shown in the figure below,
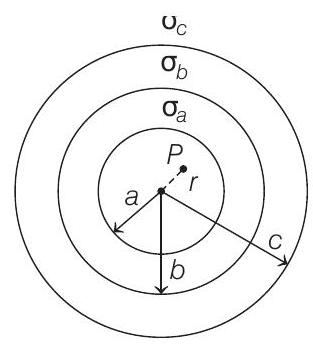
Given surface charge densities of each shell are same.
$$ \therefore \quad \sigma_{a}=\sigma_{b}=\sigma_{c} $$
As, surface charge density of shell of radius ’ $r$ ’ and having charge ’ $Q$ ’ is given as $\sigma=\frac{Q}{4 \pi r^{2}}$
So, relation (i) can be rewritten as
$$ \begin{aligned} \frac{Q_{a}}{4 \pi a^{2}} & =\frac{Q_{b}}{4 \pi b^{2}}=\frac{Q_{c}}{4 \pi c^{2}} \\ \Rightarrow \quad Q_{a}: Q_{b}: Q_{c} & =a^{2}: b^{2}: c^{2} \end{aligned} $$
where $Q_{a}, Q_{b}$ and $Q_{c}$ are charges on shell of radius $a, b$ and $c$, respectively.
Also,
$$ Q_{a}+Q_{b}+Q_{c}=Q $$
Hence,
$$ \begin{aligned} & Q_{a}=\frac{a^{2}}{a^{2}+b^{2}+c^{2}} \cdot Q \\ & Q_{b}=\frac{b^{2}}{a^{2}+b^{2}+c^{2}} \cdot Q \\ & Q_{c}=\frac{c^{2}}{a^{2}+b^{2}+c^{2}} \cdot Q \end{aligned} $$
As we know for charged spherical shell with charge $Q$ of radius ’ $R$ ‘, the potential at a point ’ $P$ ’ at distance $r$ such that $r<R$ is
$$ V_{P}=\frac{k Q}{R} . $$
$\therefore$ potential at point $P$ at a distance ’ $r$ ’ $=$ Potential due to $Q_{a}+$ Potential due to $Q_{b}+$ Potential due to $Q_{c}$
$$ =\frac{k Q_{a}}{a}+\frac{k Q_{b}}{b}+\frac{k Q_{c}}{c} $$
Substituting the values of $Q_{a}, Q_{b}$ and $Q_{c}$, we get
$$ V=\frac{Q(a+b+c)}{4 \pi \varepsilon_{0}\left(a^{2}+b^{2}+c^{2}\right)} . $$






