Electrostatics 2 Question 7
7. A charge $Q$ is distributed over three concentric spherical shells of radii $a, b, c(a<b<c)$ such that their surface charge densities are equal to one another.
The total potential at a point at distance $r$ from their common centre, where $r<a$ would be
(Main 2019, 10 Jan I)
(a) $\frac{Q\left(a^{2}+b^{2}+c^{2}\right)}{4 \pi \varepsilon _0\left(a^{3}+b^{3}+c^{3}\right)}$
(b) $\frac{Q(a+b+c)}{4 \pi \varepsilon _0\left(a^{2}+b^{2}+c^{2}\right)}$
(c) $\frac{Q}{4 \pi \varepsilon _0(a+b+c)}$
(d) $\frac{Q}{12 \pi \varepsilon _0} \cdot \frac{a b+b c+c a}{a b c}$
Show Answer
Answer:
Correct Answer: 7. (c)
Solution:
- Given charge distribution is shown in the figure below,
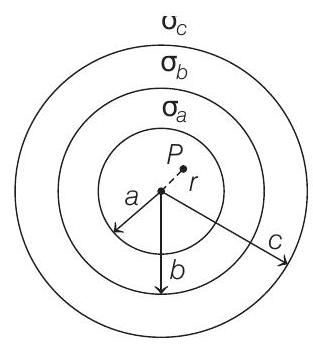
Given surface charge densities of each shell are same.
$$ \therefore \quad \sigma _a=\sigma _b=\sigma _c $$
As, surface charge density of shell of radius ’ $r$ ’ and having charge ’ $Q$ ’ is given as $\sigma=\frac{Q}{4 \pi r^{2}}$
So, relation (i) can be rewritten as
$$ \begin{aligned} \frac{Q _a}{4 \pi a^{2}} & =\frac{Q _b}{4 \pi b^{2}}=\frac{Q _c}{4 \pi c^{2}} \\ \Rightarrow \quad Q _a: Q _b: Q _c & =a^{2}: b^{2}: c^{2} \end{aligned} $$
where $Q _a, Q _b$ and $Q _c$ are charges on shell of radius $a, b$ and $c$, respectively.
Also,
$$ Q _a+Q _b+Q _c=Q $$
Hence,
$$ \begin{aligned} & Q _a=\frac{a^{2}}{a^{2}+b^{2}+c^{2}} \cdot Q \\ & Q _b=\frac{b^{2}}{a^{2}+b^{2}+c^{2}} \cdot Q \\ & Q _c=\frac{c^{2}}{a^{2}+b^{2}+c^{2}} \cdot Q \end{aligned} $$
As we know for charged spherical shell with charge $Q$ of radius ’ $R$ ‘, the potential at a point ’ $P$ ’ at distance $r$ such that $r<R$ is
$$ V _P=\frac{k Q}{R} . $$
$\therefore$ potential at point $P$ at a distance ’ $r$ ’ $=$ Potential due to $Q _a+$ Potential due to $Q _b+$ Potential due to $Q _c$
$$ =\frac{k Q _a}{a}+\frac{k Q _b}{b}+\frac{k Q _c}{c} $$
Substituting the values of $Q _a, Q _b$ and $Q _c$, we get
$$ V=\frac{Q(a+b+c)}{4 \pi \varepsilon _0\left(a^{2}+b^{2}+c^{2}\right)} . $$






