Electrostatics 2 Question 3
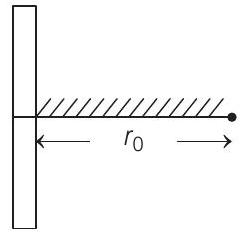
3. A positive point charge is released from rest at a distance $r_{0}$ from a positive line charge with uniform density. The speed $(v)$ of the point charge, as a function of instantaneous distance $r$ from line charge, is proportional to
(Main 2019, 8 April II)
(a) $v \propto \Big(\frac{r}{r_{0}}\Big)$
(b) $v \propto e^{+\Big(\frac{r}{r_{0}}}\Big)$
(c) $v \propto \ln \Big(\frac{r}{r_{0}}\Big)$
(d) $v \propto \sqrt{\ln \Big(\frac{r}{r_{0}}}\Big)$
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- For a positive line charge or charged wire with uniform density $\lambda$, electric field at distance $x$ is
$$ E=\frac{2 k \lambda}{x}=\frac{\lambda}{2 \pi \varepsilon_{0} x} $$
So, force on charge $q$ which is at a distance $r_{0}$ due to this line charge is $F=q E=\frac{2 k q \lambda}{x}$
…(ii) [using Eq. (i)]
Now, work done when charge is pushed by field by a small displacement $d x$ is
$$ d W=F \cdot d x=\frac{2 k q \lambda}{x} \cdot d x $$
[using Eq. (ii)]
$\therefore$ Total work done by field of wire in taking charge $q$ from distance $r_{0}$ to distance $r$ will be
$$ \begin{aligned} W & =\int_{r_{0}}^{r} d W=\int_{r_{0}}^{r} \frac{2 k q \lambda}{x} \cdot d x \\ & =2 k q \lambda[\log x]{r{0}}^{r}=2 k q \lambda\left(\log r-\log r_{0}\right) \\ & =2 k q \lambda \log \frac{r}{r_{0}} \end{aligned} . $$
As we know, from work-kinetic energy theorem,
$$ \begin{array}{cc} K_{\text {final }}-K_{\text {initial }}=W \\ \Rightarrow \quad & \frac{1}{2} m v^{2}-0=2 k q \times \log \left|\frac{r}{r_{0}}\right|^{1 / 2} \quad \text { [using Eq. (iii)] } \\ \Rightarrow \quad v=\Big(\frac{4 k q \lambda}{m} \log \Bigm\vert\frac{r}{r_{0}}\Bigm\vert\Big) \\ \therefore & v \Big(\propto \log \Bigm\vert\frac{r}{r_{0}}\Bigm\vert{ }^{1 / 2}\Big) \end{array} $$






