Electrostatics 2 Question 3
3. A positive point charge is released from rest at a distance $r _0$ from a positive line charge with uniform density. The speed $(v)$ of the point charge, as a function of instantaneous distance $r$ from line charge, is proportional to
(Main 2019, 8 April II)
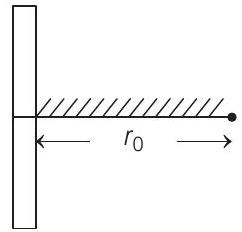
(a) $v \propto \frac{r}{r _0}$
(b) $v \propto e^{+\frac{r}{r _0}}$
(c) $v \propto \ln \frac{r}{r _0}$
(d) $v \propto \sqrt{\ln \frac{r}{r _0}}$
Show Answer
Answer:
Correct Answer: 3. (b)
Solution:
- For a positive line charge or charged wire with uniform density $\lambda$, electric field at distance $x$ is
$$ E=\frac{2 k \lambda}{x}=\frac{\lambda}{2 \pi \varepsilon _0 x} $$
So, force on charge $q$ which is at a distance $r _0$ due to this line charge is $F=q E=\frac{2 k q \lambda}{x}$
…(ii) [using Eq. (i)]
Now, work done when charge is pushed by field by a small displacement $d x$ is
$$ d W=F \cdot d x=\frac{2 k q \lambda}{x} \cdot d x $$
[using Eq. (ii)]
$\therefore$ Total work done by field of wire in taking charge $q$ from distance $r _0$ to distance $r$ will be
$$ \begin{aligned} W & =\int _{r _0}^{r} d W=\int _{r _0}^{r} \frac{2 k q \lambda}{x} \cdot d x \\ & =2 k q \lambda[\log x] _{r _0}^{r}=2 k q \lambda\left(\log r-\log r _0\right) \\ & =2 k q \lambda \log \frac{r}{r _0} \end{aligned} . $$
As we know, from work-kinetic energy theorem,
$$ \begin{array}{cc} K _{\text {final }}-K _{\text {initial }}=W \\ \Rightarrow \quad & \frac{1}{2} m v^{2}-0=2 k q \times \log \left|\frac{r}{r _0}\right|^{1 / 2} \quad \text { [using Eq. (iii)] } \\ \Rightarrow \quad v=\frac{4 k q \lambda}{m} \log \frac{r}{r _0} \\ \therefore & v \propto \log \frac{r}{r _0}{ }^{1 / 2} \end{array} $$






