Electrostatics 2 Question 26
27. Four point charges $+8 \mu \mathrm{C},-1 \mu \mathrm{C},-1 \mu \mathrm{C}$ and $+8 \mu \mathrm{C}$ are fixed at the points $-\sqrt{27 / 2} \mathrm{~m},-\sqrt{3 / 2} \mathrm{~m},+\sqrt{3 / 2} \mathrm{~m}$ and $+\sqrt{27 / 2} \mathrm{~m}$ respectively on the $y$-axis. A particle of mass $6 \times 10^{-4} \mathrm{~kg}$ and charge $+0.1 \mu \mathrm{C}$ moves along the $x$-direction. Its speed at $x=+\infty$ is $v_{0}$. Find the least value of $v_{0}$ for which the particle will cross the origin. Find also the kinetic energy of the particle at the origin. Assume that space is gravity free. $\left(1 / 4 \pi \varepsilon_{0}=9 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}\right)$.
(2000, 10 M)
Show Answer
Answer:
Correct Answer: 27. $\left(v_0\right)_{\min }=3 \mathrm{~m} / \mathrm{s}, K=3 \times 10^{-4} \mathrm{~J}$
Solution:
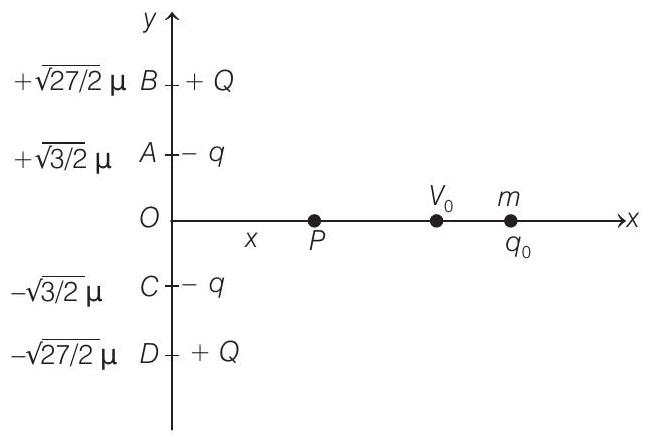
In the figure, $q=1 \mu \mathrm{C}=10^{-6} \mathrm{C}, q_{0}=+0.1 \mu \mathrm{C}=10^{-7} \mathrm{C}$
and $m=6 \times 10^{-4} \mathrm{~kg}$ and $Q=8 \mu \mathrm{C}=8 \times 10^{-6} \mathrm{C}$
Let $P$ be any point at a distance $x$ from origin $O$. Then
$$ \begin{aligned} & A P=C P=\sqrt{\frac{3}{2}+x^{2}} \\ & B P=D P=\sqrt{\frac{27}{2}+x^{2}} \end{aligned} $$
Electric potential at point $P$ will be, $V=\frac{2 K Q}{B P}-\frac{2 K q}{A P}$
where, $K=\frac{1}{4 \pi \varepsilon_{0}}=9 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}$
$$ \begin{aligned} \therefore \quad V & =2 \times 9 \times 10^{9} \frac{8 \times 10^{-6}}{\sqrt{\frac{27}{2}+x^{2}}}-\frac{10^{-6}}{\sqrt{\frac{3}{2}+x^{2}}} \\ V & =1.8 \times 10^{4} \frac{8}{\sqrt{\frac{27}{2}+x^{2}}}-\frac{1}{\sqrt{\frac{3}{2}+x^{2}}} \end{aligned} $$
$\therefore \quad$ Electric field at point $P$ is
$$ \begin{array}{r} E=-\frac{d V}{d X}=1.8 \times 10^{4} \text { (8) } \frac{-1}{2} \quad \frac{27}{2}+x^{2} \\ -\frac{1}{2} \quad \frac{3}{2}+x^{2} \end{array} $$
$E=0$ on $x$-axis where $x=0$,
or $\quad \frac{8}{\frac{27}{2}+x^{2}}=\frac{1}{\frac{3}{2}+x^{2}}$
$\Rightarrow \quad \frac{(4)^{3 / 2}}{\frac{27}{2}+x^{2}}{ }^{3 / 2}=\frac{1}{\frac{3}{2}+x^{2}}$
$\Rightarrow \quad \frac{27}{2}+x^{2}=4 \frac{3}{2}+x^{2}$
This equation gives, $x= \pm \sqrt{\frac{5}{2}} \mathrm{~m}$
The least value of kinetic energy of the particle at infinity should be enough to take the particle upto $x=+\sqrt{\frac{5}{2}} \mathrm{~m}$ because at $x=+\sqrt{\frac{5}{2}} \mathrm{~m}, E=0$.
$\Rightarrow$ Electrostatic force on charge $q$ is zero or $F_{e}=0$.
For at $x>\sqrt{\frac{5}{2}} \mathrm{~m}, E$ is repulsive (towards positive $x$-axis)
and for $x<\sqrt{\frac{5}{2}} \mathrm{~m}, E$ is attractive (towards negative $x$-axis)
Now, from Eq. (i), potential at $x=\sqrt{\frac{5}{2}} \mathrm{~m}$
$$ V=1.8 \times 10^{4} \frac{8}{\sqrt{\frac{27}{2}+\frac{5}{2}}}-\frac{1}{\sqrt{\frac{3}{2}+\frac{5}{2}}} $$
$$ V=2.7 \times 10^{4} \mathrm{~V} $$
Applying energy conservation at $x=\infty$ and $x=\sqrt{\frac{5}{2}} \mathrm{~m}$
$$ \begin{aligned} \frac{1}{2} m v_{0}^{2} & =q_{0} V \\ \therefore \quad v_{0} & =\sqrt{\frac{2 q_{0} V}{m}} \end{aligned} $$
Substituting these values,
$$ v_{0}=\sqrt{\frac{2 \times 10^{-7} \times 2.7 \times 10^{4}}{6 \times 10^{-4}}} . \Rightarrow v_{0}=3 \mathrm{~m} / \mathrm{s} $$
$\therefore$ Minimum value of $v_{0}$ is $3 \mathrm{~m} / \mathrm{s}$
From Eq. (i), potential at origin $(x=0)$ is
$$ V_{0}=1.8 \times 10^{4} \frac{8}{\sqrt{\frac{27}{2}}}-\frac{1}{\sqrt{\frac{3}{2}}} \approx 2.4 \times 10^{4} \mathrm{~V} $$
Let $K$ be the kinetic energy of the particle at origin. Applying energy conservation at $x=0$ and at $x=\infty$
$$ K+q_{0} V_{0}=\frac{1}{2} m v_{0}^{2} $$
But $\quad \frac{1}{2} m v_{0}^{2}=q_{0} V$ [from Eq. (ii)]
$$ \begin{aligned} & K=q_{0}\left(V-V_{0}\right) \\ & K=\left(10^{-7}\right)\left(2.7 \times 10^{4}-2.4 \times 10^{4}\right) \\ & K=3 \times 10^{-4} \mathrm{~J} \end{aligned} $$
NOTE
$E=0$ or $F_{e}$ on $q_{0}$ is zero at $x=0$ and $x= \pm \sqrt{\frac{5}{2}} \mathrm{~m}$ of
these $x=0$ is stable equilibrium position and $x= \pm \sqrt{\frac{5}{2}}$ is unstable equilibrium position.






