Electrostatics 2 Question 1
1. In free space, a particle $A$ of charge $1 \mu \mathrm{C}$ is held fixed at a point $P$. Another particle $B$ of the same charge and mass $4 \mu \mathrm{g}$ is kept at a distance of $1 \mathrm{~mm}$ from $P$. If $B$ is released, then its velocity at a distance of $9 \mathrm{~mm}$ from $P$ is
[Take, $\frac{1}{4 \pi \varepsilon_{0}}=9 \times 10^{9} \mathrm{~N}-\mathrm{m}^{2} \mathrm{C}^{-2}$]
(Main 2019, 10 April II)
(a) $1.5 \times 10^{2} \mathrm{~m} / \mathrm{s}$
(b) $3.0 \times 10^{4} \mathrm{~m} / \mathrm{s}$
(c) $1.0 \mathrm{~m} / \mathrm{s}$
(d) $2.0 \times 10^{3} \mathrm{~m} / \mathrm{s}$
Show Answer
Answer:
Correct Answer: 1. (d)
Solution:
- Given situation is shown in the figure below,
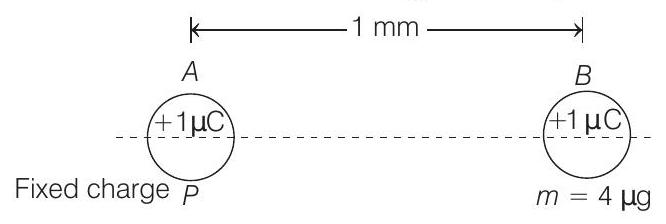
When charged particle $B$ is released due to mutual repulsion, it moves away from $A$. In this process, potential energy of system of charges reduces and this change of potential energy appears as kinetic energy of $B$.
Now, potential energy of system of charges at separation of $1 \mathrm{~mm}$ is
$$ \begin{aligned} & U_{1}=\frac{K q_{1} q_{2}}{r} \\ & q_{1}=q_{2}=1 \times 10^{-6} \mathrm{C} \\ & \therefore \quad U_{1}=\frac{9 \times 10^{9} \times 1 \times 10^{-6} \times 1 \times 10^{-6}}{1 \times 10^{-3}}=9 \mathrm{~J} \end{aligned} $$
Potential energy of given system of charges at separation of $9 \mathrm{~mm}$ is
$$ U_{2}=\frac{K q_{1} q_{2}}{r}=\frac{9 \times 10^{9} \times\left(1 \times 10^{-6}\right)^{2}}{9 \times 10^{-3}}=1 \mathrm{~J} $$
By energy conservation,
Change in potential energy of system of $A$ and $B$
$$ =\text { Kinetic energy of charged particle } B $$
$$ \Rightarrow \quad U_{1}-U_{2}=\frac{1}{2} m_{B} v_{B}^{2} $$
where, $m_{B}=$ mass of particle $B=4 \mu \mathrm{g}$
$$ =4 \times 10^{-6} \times 10^{-3} \mathrm{~kg}=4 \times 10^{-9} \mathrm{~kg} $$
and $v_{B}=$ velocity of particle $B$ at separation of
$9 \mathrm{~mm}$
$$ \begin{aligned} & \Rightarrow \quad 9-1=\frac{1}{2} \times 4 \times 10^{-9} \times v_{B}^{2} \\ & \Rightarrow \quad v_{B}^{2}=4 \times 10^{9} \Rightarrow v_{B}=2 \times 10^{3} \mathrm{~ms}^{-1} \end{aligned} $$






