SATHEE: Electrostatics 2 Question 1

Electrostatics 2 Question 1

1. In free space, a particle $A$ of charge $1 μ C$ is held fixed at a point $P$ . Another particle $B$ of the same charge and mass $4 μ g$ is kept at a distance of $1 m m$ from $P$ . If $B$ is released, then its velocity at a distance of $9 m m$ from $P$ is

Take, $\frac{1}{4 π ε_{0}} = 9 \times 10^{9} N - m^{2} C^{- 2}$

(Main 2019, 10 April II)

(a) $1.5 \times 10^{2} m / s$

(b) $3.0 \times 10^{4} m / s$

(d) $2.0 \times 10^{3} m / s$

Show Answer

Answer:

Correct Answer: 1. (b)

Solution:

Given situation is shown in the figure below,

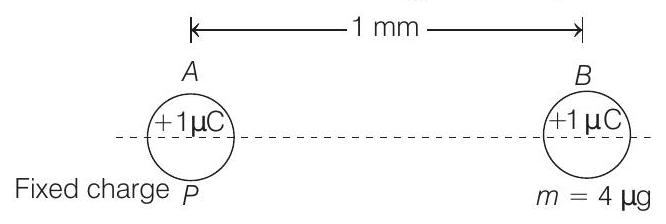
When charged particle $B$ is released due to mutual repulsion, it moves away from $A$ . In this process, potential energy of system of charges reduces and this change of potential energy appears as kinetic energy of $B$ .

Now, potential energy of system of charges at separation of $1 m m$ is

$\begin{aligned} U_{1} = \frac{K q_{1} q_{2}}{r} \\ q_{1} = q_{2} = 1 \times 10^{- 6} C \\ ∴ U_{1} = \frac{9 \times 10^{9} \times 1 \times 10^{- 6} \times 1 \times 10^{- 6}}{1 \times 10^{- 3}} = 9 J \end{aligned}$

Potential energy of given system of charges at separation of $9 m m$ is

$U_{2} = \frac{K q_{1} q_{2}}{r} = \frac{9 \times 10^{9} \times {(1 \times 10^{- 6})}^{2}}{9 \times 10^{- 3}} = 1 J$

By energy conservation,

Change in potential energy of system of $A$ and $B$

$= Kinetic energy of charged particle B$

$\Rightarrow U_{1} - U_{2} = \frac{1}{2} m_{B} v_{B}^{2}$

where, $m_{B} =$ mass of particle $B = 4 μ g$

$= 4 \times 10^{- 6} \times 10^{- 3} k g = 4 \times 10^{- 9} k g$

and $v_{B} =$ velocity of particle $B$ at separation of

$9 m m$

$\begin{aligned} \Rightarrow 9 - 1 = \frac{1}{2} \times 4 \times 10^{- 9} \times v_{B}^{2} \\ \Rightarrow v_{B}^{2} = 4 \times 10^{9} \Rightarrow v_{B} = 2 \times 10^{3} m s^{- 1} \end{aligned}$