Electromagnetic Induction and Alternating Current 7 Question 5
####5. An $L-C-R$ circuit is equivalent to a damped pendulum. In an $L-C-R$ circuit, the capacitor is charged to $Q_{0}$ and then connected to the $L$ and $R$ as shown.
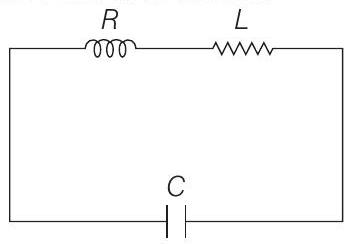
If a student plots graphs of the square of maximum charge $\left(Q_{\text {Max }}^{2}\right)$ on the capacitor with time $(\mathrm{t})$ for two different values $L_{1}$ and $L_{2}\left(L_{1}>L_{2}\right)$ of $\mathrm{L}$, then which of the following represents this graph correctly? (plots are schematic and not drawn to scale)
(2015 Main)
(a)

(b)
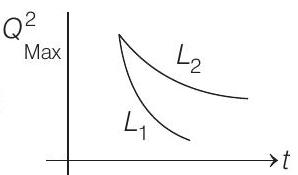
(c)

(d)
Show Answer
Answer:
Correct Answer: 5. (d)
Solution:
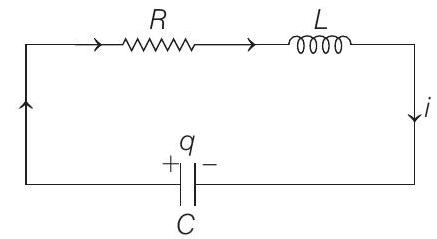
At a general time $t$, suppose charge on capacitor is $q$ and current in the circuit is $i$, then applying Kirchhoff’s loop law, we have
Putting
$$ \frac{q}{c}-i R-L \frac{d i}{d t}=0 $$
In the above equation, we have
$$ \frac{d^{2} q}{d t^{2}}+\frac{R}{L} \frac{d q}{d t}+\frac{q}{L C}=0 $$
Comparing this equation with the standard differential equation of damped oscillation,
$$ \frac{d^{2} X}{d t^{2}}+\frac{b}{m} \frac{d X}{d t}+\frac{K}{m} X=0 $$
Which has a general solution of amplitude, $A=A_{0} e^{\frac{-b t}{2 m}}$ The general solution of Eq. (i) will be
$$ Q_{\max }=Q_{0} e^{\frac{-R t}{2 L}} \text { or } Q_{\max }^{2}=Q_{0}^{2} e^{\frac{-R t}{L}} $$
Hence, $Q_{\max }^{2}$ versus time graph is exponentially decreasing graph. Lesser the value of self inductance, faster will be the damping.






