Electromagnetic Induction and Alternating Current 7 Question 12
12. A coil of wire having finite inductance and resistance has a conducting ring placed co-axially within it. The coil is connected to a battery at time $t=0$, so that a time dependent current $I _1(t)$ starts flowing through the coil. If $I _2(t)$ is the current induced in the ring and $B(t)$ is the magnetic field at the axis of the coil due to $I _1(t)$, then as a function of time $(t>0)$, the product $I _2(t) B(t)$
$(2000,2 M)$
(a) increases with time
(b) decreases with time
(c) does not vary with time
(d) passes through a maximum
Show Answer
Answer:
Correct Answer: 12. (d)
Solution:
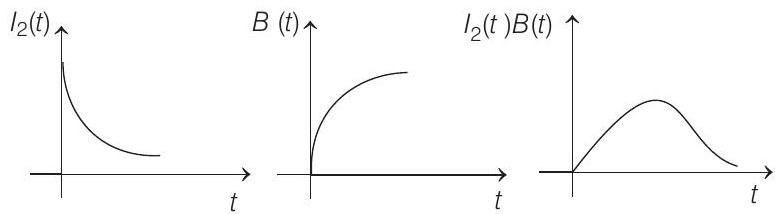
- The equations of $I _1(t), I _2(t)$ and $B(t)$ will take the following forms :
$$ \begin{aligned} & I _1(t)=K _1\left(1-e^{-k _2 t}\right) \rightarrow \text { current growth in } L-R \text { circuit } \\ & B(t)=K _3\left(1-e^{-k _2 t}\right) \rightarrow B(t) \propto I _1(t) \\ & I _2(t)=K _4 e^{-k _2 t} \\ & I _2(t)=\frac{e _2}{R} \text { and } e _2 \propto \frac{d I _1}{d t}: e _2=-M \frac{d I _1}{d t} \end{aligned} $$
Therefore, the product $I _2(t) B(t)=K _5 e^{-k _2 t}\left(1-e^{-k _2 t}\right)$. The value of this product is zero at $t=0$ and $t=\infty$. Therefore, the product will pass through a maximum value. The corresponding graphs will be as follows :