Electromagnetic Induction and Alternating Current 6 Question 7
####7. When an AC source of emf $e=E_{0}$ $\sin (100 t)$ is connected across a circuit, the phase difference between the emf $e$ and the current $i$ in the circuit is observed to be $\frac{\pi}{4}$
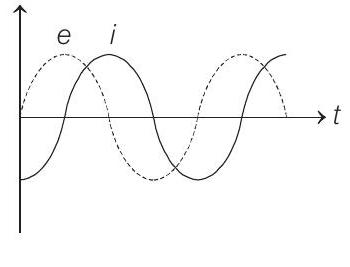ahead, as shown in the diagram. If the circuit consists possibly only of $R-C$ or $R-L$ or $L-C$ in series, find the relationship between the two elements.
(2003, 2M)
(a) $R=1 \mathrm{k} \Omega, C=10 \mu \mathrm{F}$
(b) $R=1 \mathrm{k} \Omega, C=1 \mu \mathrm{F}$
(c) $R=1 \mathrm{k} \Omega, L=10 \mathrm{H}$
(d) $R=1 \mathrm{k} \Omega, L=1 \mathrm{H}$
Show Answer
Answer:
Correct Answer: 7. (a)
Solution:
- As the current $i$ leads the emf $e$ by $\pi / 4$, it is an $R-C$ circuit.
$$ \begin{array}{rlrl} & & \tan \varphi & =\frac{X_{C}}{R} \\ & \text { or } & \tan \frac{\pi}{4} & =\frac{1}{\omega C} \\ & \therefore & \omega C R & =1 \\ \text { As } & \omega & =100 \mathrm{rad} / \mathrm{s} \end{array} $$
The product of $C-R$ should be $\frac{1}{100} \mathrm{~s}^{-1}$
Option (a) satisfy this condition.
