Electromagnetic Induction and Alternating Current 6 Question 2
2. An alternating voltage $V(t)=220 \sin 100 \pi t$ volt is applied to a purely resistive load of $50 \Omega$. The time taken for the current to rise from half of the peak value to the peak value is
(a) $5 ms$
(b) $2.2 ms$
(c) $7.2 ms$
(d) $3.3 ms$
Show Answer
Answer:
Correct Answer: 2. (d)
Solution:
- In an $AC$ resistive circuit, current and voltage are in phase.
$$ \begin{array}{ll} \text { So, } & I=\frac{V}{R} \\ \Rightarrow & I=\frac{220}{50} \sin (100 \pi t) \end{array} $$
$\therefore$ Time period of one complete cycle of current is
$$ T=\frac{2 \pi}{\omega}=\frac{2 \pi}{100 \pi}=\frac{1}{50} s $$
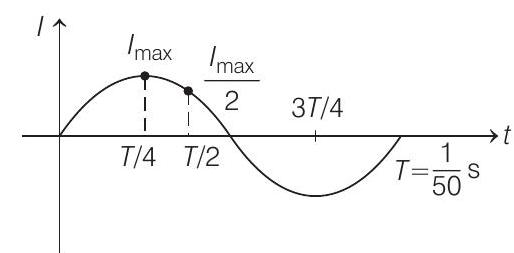
So, current reaches its maximum value at
$$ t _1=\frac{T}{4}=\frac{1}{200} s $$
When current is half of its maximum value, then from Eq. (i), we have
$$ I=\frac{I _{\max }}{2}=I _{\max } \sin \left(100 \pi t _2\right) $$
$\Rightarrow \sin \left(100 \pi t _2\right)=\frac{1}{2} \Rightarrow 100 \pi t _2=\frac{5 \pi}{6}$
So, instantaneous time at which current is half of maximum value is $t _2=\frac{1}{120} s$
Hence, time duration in which current reaches half of its maximum value after reaching maximum value is
$$ \Delta t=t _2-t _1=\frac{1}{120}-\frac{1}{200}=\frac{1}{300} s=3.3 ms $$






