SATHEE: Electromagnetic Induction and Alternating Current 6 Question 2

Electromagnetic Induction and Alternating Current 6 Question 2

2. An alternating voltage $V (t) = 220 \sin 100 π t$ volt is applied to a purely resistive load of $50 Ω$ . The time taken for the current to rise from half of the peak value to the peak value is

(a) $5 m s$

(b) $2.2 m s$

(d) $3.3 m s$

Show Answer

Answer:

Correct Answer: 2. (d)

Solution:

In an $A C$ resistive circuit, current and voltage are in phase.

$\begin{array}{ll} So, & I = \frac{V}{R} \\ \Rightarrow & I = \frac{220}{50} \sin (100 π t) \end{array}$

$∴$ Time period of one complete cycle of current is

$T = \frac{2 π}{ω} = \frac{2 π}{100 π} = \frac{1}{50} s$

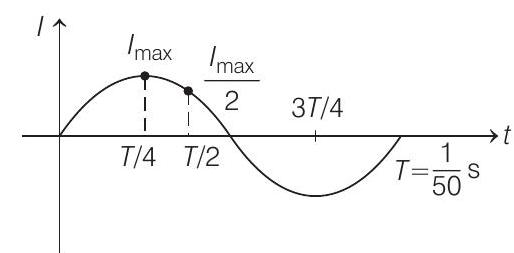
So, current reaches its maximum value at

$t_{1} = \frac{T}{4} = \frac{1}{200} s$

When current is half of its maximum value, then from Eq. (i), we have

$I = \frac{I_{max}}{2} = I_{max} \sin (100 π t_{2})$

$\Rightarrow \sin (100 π t_{2}) = \frac{1}{2} \Rightarrow 100 π t_{2} = \frac{5 π}{6}$

So, instantaneous time at which current is half of maximum value is $t_{2} = \frac{1}{120} s$

Hence, time duration in which current reaches half of its maximum value after reaching maximum value is

$Δ t = t_{2} - t_{1} = \frac{1}{120} - \frac{1}{200} = \frac{1}{300} s = 3.3 m s$

पिछला

अगला

Electromagnetic Induction and Alternating Current 6 Question 2

2. An alternating voltage $V (t) = 220 \sin 100 π t$ volt is applied to a purely resistive load of $50 Ω$ . The time taken for the current to rise from half of the peak value to the peak value is

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Electromagnetic Induction and Alternating Current 6 Question 2

2. An alternating voltage V(t)=220sin⁡100πt volt is applied to a purely resistive load of 50Ω. The time taken for the current to rise from half of the peak value to the peak value is

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

2. An alternating voltage $V (t) = 220 \sin 100 π t$ volt is applied to a purely resistive load of $50 Ω$ . The time taken for the current to rise from half of the peak value to the peak value is