Electromagnetic Induction and Alternating Current 4 Question 22
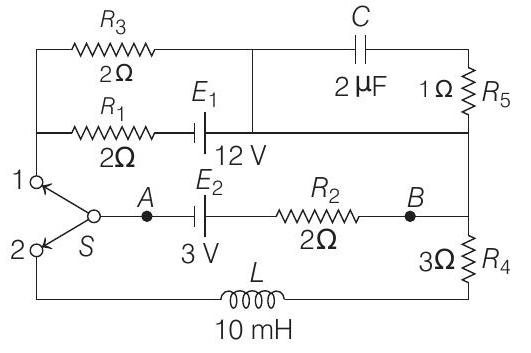
####22. A circuit containing a two position switch $S$ is shown in figure.
(1991, 4+4M)
(a) The switch $S$ is in position 1. Find the potential difference $V_{A}-V_{B}$ and the rate of production of joule heat in $R_{1}$.
(b) If now the switch $S$ is put in position 2 at $t=0$. Find
(i) steady current in $R_{4}$ and
(ii) the time when current in $R_{4}$ is half the steady value. Also, calculate the energy stored in the inductor $L$ at that time.
Show Answer
Answer:
Correct Answer: 22. $(a) $-5V , 24.5W $
(b) (i) $0.6A $
(ii) $1.386 \times {10} ^{-3} s$, $4.5 \times {10} ^{-4} J$
Solution:
- (a) In steady state, no current will flow through capacitor. Applying Kirchhoff’s second law in loop 1
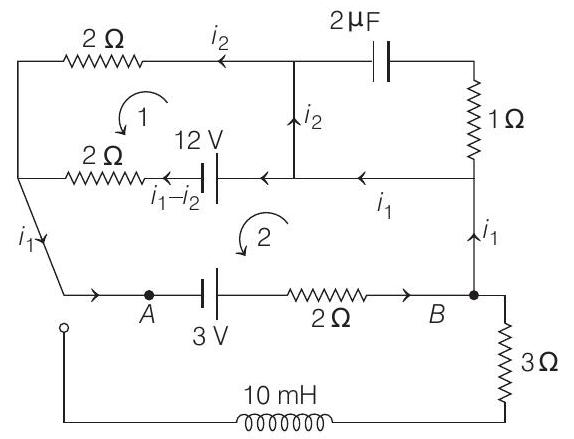
$$ \begin{aligned} & -2 i_{2}+2\left(i_{1}-i_{2}\right)+12=0 \\ & \therefore \quad 2 i_{1}-4 i_{2}=-12 \\ & \text { or } \quad i_{1}-2 i_{2}=-6 \end{aligned} $$
Applying Kirchhoff’s second law in loop 2
$$ -12-2\left(i_{1}-i_{2}\right)+3-2 i_{1}=0 $$
$$ \therefore \quad 4 i_{1}-2 i_{2}=-9 $$
Solving Eqs. (i) and (ii), we get
$$ \begin{aligned} i_{2} & =2.5 \mathrm{~A} \text { and } i_{1}=-1 \mathrm{~A} \\ \text { Now, } V_{A}+3-2 i_{1} & =V_{B} \\ \text { or } V_{A}-V_{B}=2 i_{1}-3 & =2(-1)-3=-5 \mathrm{~V} \\ P_{R_{1}}=\left(i_{1}-i_{2}\right)^{2} R_{1} & =(-1-2.5)^{2}(2)=24.5 \mathrm{~W} \end{aligned} $$
(b) In position 2 : Circuit is as under
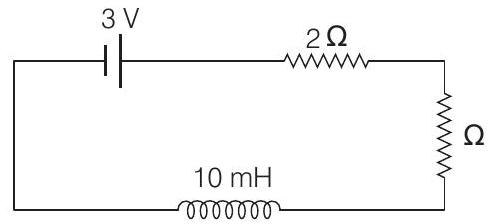
(i) Steady current in $R_{4}$ :
$$ i_{0}=\frac{3}{3+2}=0.6 \mathrm{~A} $$
(ii) Time when current in $R_{4}$ is half the steady value
$$ \begin{aligned} t_{1 / 2} & =\tau_{L}(\ln 2)=\frac{L}{R} \ln (2) \\ & =\frac{\left(10 \times 10^{-3}\right)}{5} \ln (2) \\ & =1.386 \times 10^{-3} \mathrm{~s} \\ U & =\frac{1}{2} L i^{2}=\frac{1}{2}\left(10 \times 10^{-3}\right)(0.3)^{2} \\ & =4.5 \times 10^{-4} \mathrm{~J} \end{aligned} $$






