Electromagnetic Induction and Alternating Current 4 Question 22
####22. A circuit containing a two position switch
(1991, 4+4M)
(a) The switch
(b) If now the switch
(i) steady current in
(ii) the time when current in
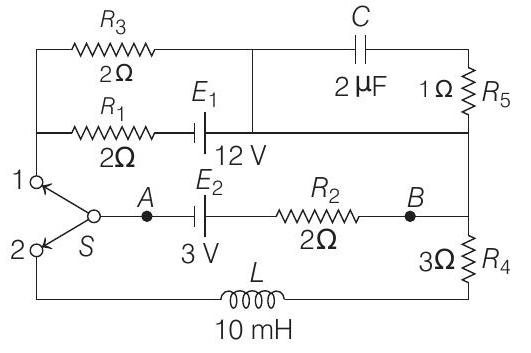
Show Answer
Answer:
Correct Answer: 22.
(b) (i)
(ii)
Solution:
- (a) In steady state, no current will flow through capacitor. Applying Kirchhoff’s second law in loop 1
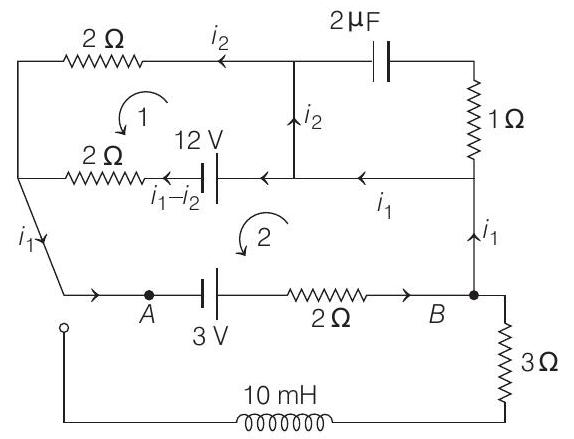
Applying Kirchhoff’s second law in loop 2
Solving Eqs. (i) and (ii), we get
(b) In position 2 : Circuit is as under
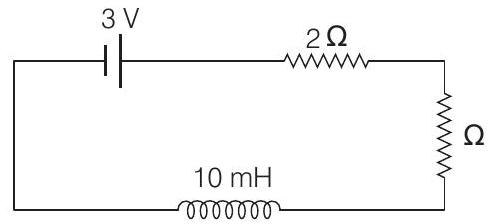
(i) Steady current in
(ii) Time when current in






