Electromagnetic Induction and Alternating Current 4 Question 18
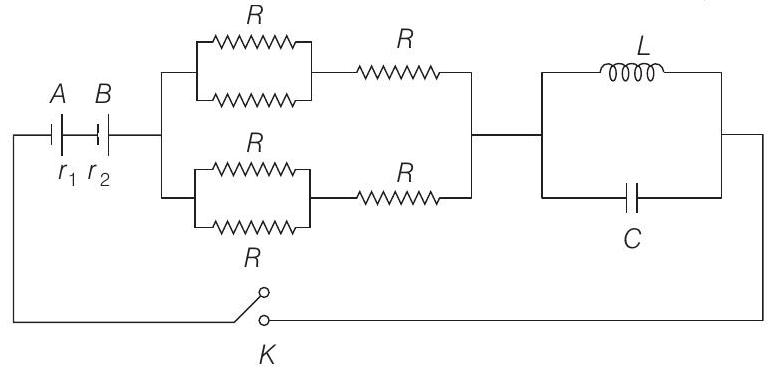
####18. In the circuit shown $A$ and $B$ are two cells of same emf $E$ but different internal resistances $r_{1}$ and $r_{2}\left(r_{1}>r_{2}\right)$ respectively. Find the value of $R$ such that the potential difference across the terminals of cell $A$ is zero, a long time after the key $K$ is closed.
$(2004,4 M)$
Show Answer
Answer:
Correct Answer: 18. $R=\frac{4}{3}(r_1-r_2)$
Solution:
- After a long time, resistance across an inductor becomes zero while resistance across capacitor becomes infinite. Hence, net external resistance,
$$ R_{\mathrm{net}}=\frac{\frac{R}{2}+R}{2}=\frac{3 R}{4} $$
Current through the batteries, $i=\frac{2 E}{\frac{3 R}{4}+r_{1}+r_{2}}$
Given that potential across the terminals of cell $A$ is zero.
$$ \begin{aligned} & \therefore \quad E-i r_{1}=0 \\ & \text { or } \quad E-\frac{2 E}{3 R / 4+r_{1}+r_{2}} r_{1}=0 \end{aligned} $$
Solving this equation, we get, $R=\frac{4}{3}\left(r_{1}-r_{2}\right)$






