Electromagnetic Induction and Alternating Current 4 Question 18
####18. In the circuit shown
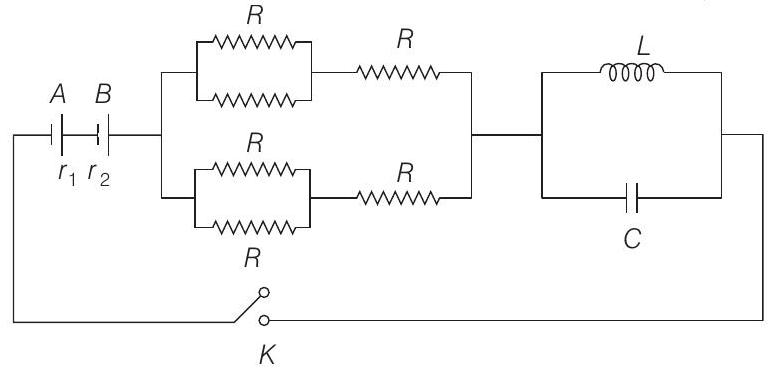
Show Answer
Answer:
Correct Answer: 18.
Solution:
- After a long time, resistance across an inductor becomes zero while resistance across capacitor becomes infinite. Hence, net external resistance,
Current through the batteries,
Given that potential across the terminals of cell
Solving this equation, we get,






