Electromagnetic Induction and Alternating Current 2 Question 8
9. A pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is $L$. A conducting massless rod of resistance $R$ can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table. A mass $m$ tied to the other end of the string hangs vertically. A constant magnetic field $B$ exists perpendicular to the table. If the system is released from rest. Calculate :
(1997, 5M)
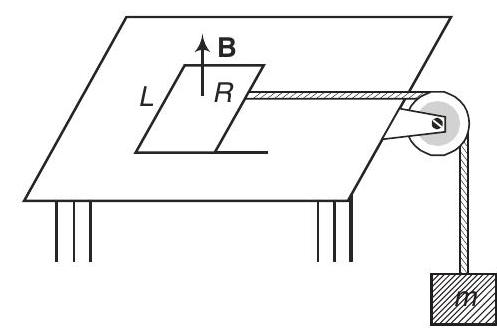
(a) the terminal velocity achieved by the rod, and
(b) the acceleration of the mass at the instant when the velocity of the rod is half the terminal velocity.
Show Answer
Answer:
Correct Answer: 9. (a) $v _T=\frac{m g R}{B^{2} L^{2}}$ (b) $a=\frac{g}{2}$
Solution:
- (a) Let $v$ be the velocity of the wire (as well as block) at any instant of time $t$.
Motional emf, $e=B v L$
Motional current, $i=\frac{e}{r}=\frac{B v L}{R}$
and magnetic force on the wire
$$ F _m=i L B=\frac{v B^{2} L^{2}}{R} $$
Net force in the system at this moment will be
$$ \begin{aligned} F _{\text {net }} & =m g-F _m=m g-\frac{v B^{2} L^{2}}{R} \\ \text { or } \quad m a & =m g-\frac{v B^{2} L^{2}}{R} \\ a & =g-\frac{v B^{2} L^{2}}{m R} \end{aligned} $$
Velocity will acquire its terminal value i.e. $v=v _T$ when $F _{\text {net }}$ or acceleration ( $a$ ) of the particle becomes zero.
$$ \begin{array}{ll} \text { Thus, } & 0=g-\frac{v _T B^{2} L^{2}}{m R} \\ \text { or } & v _T=\frac{m g R}{B^{2} L^{2}} \\ \text { When } & v=\frac{v _T}{2}=\frac{m g R}{2 B^{2} L^{2}} \end{array} $$
(b) When
Then from Eq. (i), acceleration of the block,
$$ a=g-\frac{m g R}{2 B^{2} L^{2}} \quad \frac{B^{2} L^{2}}{m R}=g-\frac{g}{2} $$
or
$$ a=\frac{g}{2} $$






