Electromagnetic Induction and Alternating Current 1 Question 15
15. A rectangular frame $A B C D$, made of a uniform metal wire, has a straight connection between $E$ and $F$ made of the same wire, as shown in figure. $A E F D$ is a square of side $1 m$ and $E B$ $=F C=0.5 m$. The entire circuit is placed in a steadily increasing uniform magnetic field directed into the plane of the paper and normal to it.
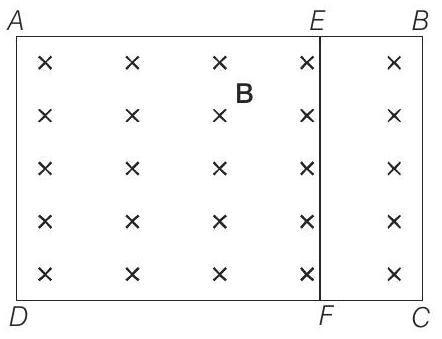
The rate of change of the magnetic field is $1 T / s$. The resistance per unit length of the wire is $1 \Omega / m$. Find the magnitudes and directions of the currents in the segments $A E$, $B E$ and $E F$.
(1993, 5M)
Show Answer
Answer:
Correct Answer: 15. $\frac{7}{22} A(E$ to $A), \frac{6}{22} A(B$ to $E), \frac{1}{22} A(F$ to $E)$
Solution:
- Induced emf in two loops $A E F D$ and $E B C F$ would be
$$ e _1=\frac{d \varphi _1}{d t}=S _1 \frac{d B}{d t}=(1 \times 1)(1) V=1 V $$
Similarly, $e _2=\frac{d \varphi _2}{d t}=S _2 \frac{d B}{d t}=(0.5 \times 1)(1) V=0.5 V$
Now, since the magnetic field is increasing, the induced current will produce the magnetic field in $U$ direction. Hence, $e _1$ and $e _2$ will be applied as shown in the figure.
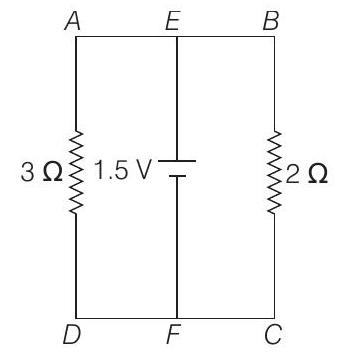
Kirchhoff’s first law at junction $F$ gives
$$ i _1=i+i _2 $$
Kirchhoff’s second law in loop FEADF gives
$$ 3 i _1+i=1 $$
Kirchhoff’s second law in loop $F E B C F$ gives
$$ 2 i _2-i=0.5 $$
Solving Eqs. (i), (ii) and (iii), we get
$$ \begin{aligned} i _1 & =\frac{7}{22} A \text { and } i _2=\frac{6}{22} A \\ \text { and } \quad i & =(1 / 22) A \end{aligned} $$
Therefore, current in segment $A E$ is (7/22) A from $E$ to $A$, current in segment $B E$ is $6 / 22 A$ from $B$ to $E$ and current in segment $E F$ is (1/22) A from $F$ to $E$.
