Electromagnetic Induction and Alternating Current 1 Question 1
####1. A very long solenoid of radius $R$ is carrying current $I(t)=k t e^{-\alpha t}(k>0)$, as a function of time $(t \geq 0)$. Counter clockwise current is taken to be positive. A circular conducting coil of radius $2 R$ is placed in the equatorial plane of the solenoid and concentric with the solenoid. The current induced in the outer coil is correctly depicted, as a function of time, by
(Main 2019, 9 April II)
(a)
(b)
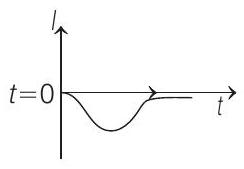
(c)
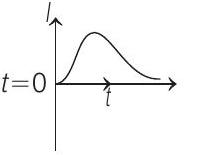
(d)
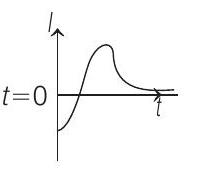
Show Answer
Answer:
Correct Answer: 1. (d)
Solution:
- Magnetic flux associated with the outer coil is
$$ \begin{aligned} \varphi_{\text {outer }} & =\mu_{0} \pi N R \cdot I=\mu_{0} N \pi R\left(k t e^{-\alpha t}\right) \\ & =C t e^{-\alpha t} \end{aligned} $$
where,
$$ C=\mu_{0} N \pi R k=\mathrm{constant} $$
Induced emf,
$$ \begin{aligned} e & =\frac{-d \varphi_{\text {outer }}}{d t}=C e^{-\alpha t}+\left(-\alpha C t e^{-\alpha t}\right) \\ & =C e^{-\alpha t}(1-\alpha t) \end{aligned} $$
$\therefore$ Induced current, $I=\frac{e}{\text { Resistance }}$
$$ \Rightarrow \quad \text { At } t=0, I=-\mathrm{ve} $$
$\therefore$ The correct graph representing this condition is given in option (d).
Alternate Solution
Given solenoid is shown below as,
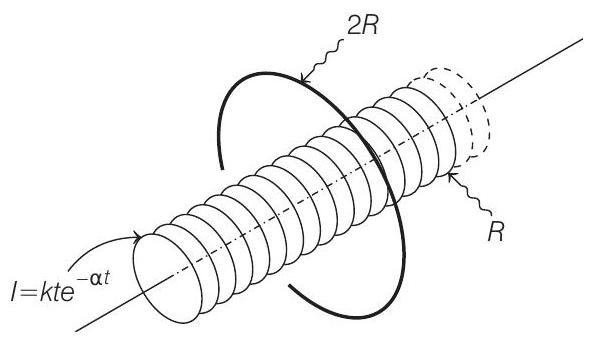
At $t=0$, current in solenoid
$$ =I(t=0)=k(0) e^{-\alpha \cdot 0}=0 $$
Graph of $e^{\alpha t}$ and $k t$ versus time can be shown as,
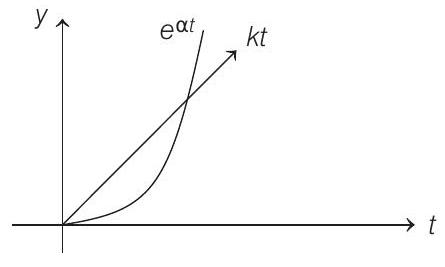
$$ \begin{array}{ll} \text { As, } & I=\frac{k t}{e^{\alpha t}} \\ \text { Initially, } & k t>e^{\alpha t} \end{array} $$
So, current is increasing in magnitude.
Finally, after a short time $k t<e^{\alpha t}$. So, current is decreasing in magnitude.
But in both cases, it remains positive or counter clockwise. So, current induced is at first anti-clockwise (following Lenz’s law) and then it becomes clockwise and finally reduces to zero as $t \rightarrow \infty$.
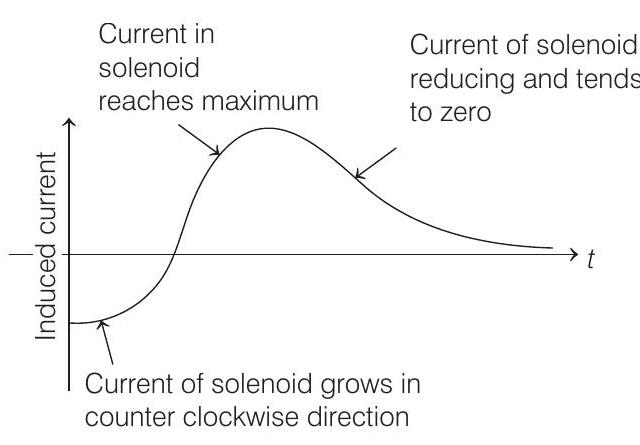
So, correct graph of induced current is






