Electromagnetic Induction and Alternating Current 1 Question 1
####1. A very long solenoid of radius
(Main 2019, 9 April II)
(a)
(b)
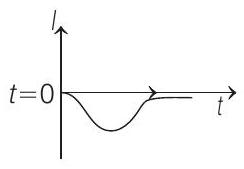
(c)
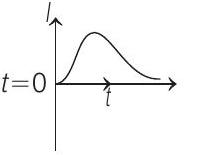
(d)
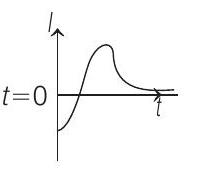
Show Answer
Answer:
Correct Answer: 1. (d)
Solution:
- Magnetic flux associated with the outer coil is
where,
Induced emf,
Alternate Solution
Given solenoid is shown below as,
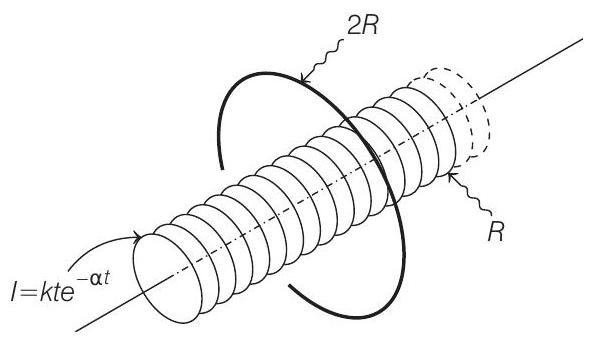
At
Graph of
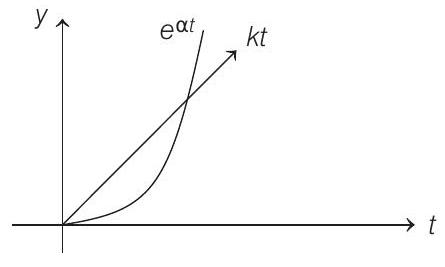
So, current is increasing in magnitude.
Finally, after a short time
But in both cases, it remains positive or counter clockwise. So, current induced is at first anti-clockwise (following Lenz’s law) and then it becomes clockwise and finally reduces to zero as
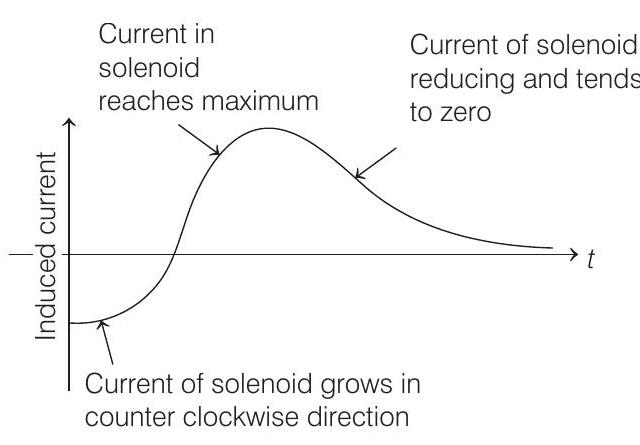
So, correct graph of induced current is






