Current Electricity 1 Question 1
1. Space between two concentric conducting spheres of radii $a$ and $b(b>a)$ is filled with a medium of resistivity $\rho$. The resistance between the two spheres will be
(a) $\frac{\rho}{2 \pi} \frac{1}{a}+\frac{1}{b}$
(b) $\frac{\rho}{4 \pi} \frac{1}{a}-\frac{1}{b}$
(c) $\frac{\rho}{2 \pi} \frac{1}{a}-\frac{1}{b}$
(d) $\frac{\rho}{4 \pi} \frac{1}{a}+\frac{1}{b}$
(2019 Main, 10 April II)
Show Answer
Solution:
- Key Idea Resistance between surface of inner shell and a circumferential point of outer shell can be formed by finding resistance of a thin (differentially thin) shell in between these two shells. Then, this result can be integrated (summed up) to get resistance of the complete arrangement.
For an elemental shell of radius $x$ and thickness $d x$,
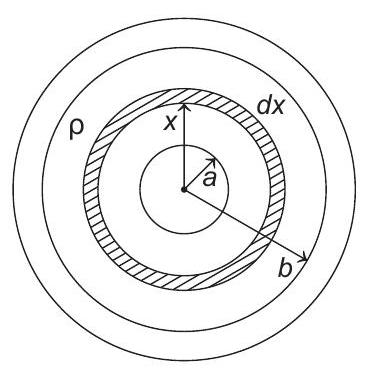
Resistance, $\quad d R=\rho \frac{l}{A}$
$$ \Rightarrow \quad d R=\rho \frac{d x}{4 \pi x^{2}} $$
So, resistance of complete arrangement is
$$ \begin{aligned} R & =\int _a^{b} d R=\int _a^{b} \rho \frac{d x}{4 \pi x^{2}}=\frac{\rho}{4 \pi} \int _a^{b} x^{-2} d x \\ \Rightarrow \quad R & =\frac{\rho}{4 \pi} \frac{x^{-1}}{-1}=\frac{\rho}{4 \pi}-\frac{1}{x}{ } _a^{b} \\ & =\frac{\rho}{4 \pi}-\frac{1}{b}–\frac{1}{a}=\frac{\rho}{4 \pi} \frac{1}{a}-\frac{1}{b} \text { ohm } \end{aligned} $$






