Current Electricity 1 Question 1
1. Space between two concentric conducting spheres of radii
(a)
(b)
(c)
(d)
(2019 Main, 10 April II)
Show Answer
Solution:
- Key Idea Resistance between surface of inner shell and a circumferential point of outer shell can be formed by finding resistance of a thin (differentially thin) shell in between these two shells. Then, this result can be integrated (summed up) to get resistance of the complete arrangement.
For an elemental shell of radius
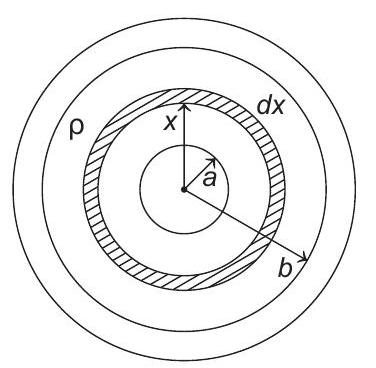
Resistance,
So, resistance of complete arrangement is






