Centre of Mass 3 Question 35
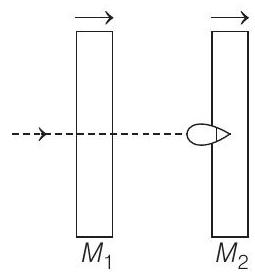
38. A $20 g$ bullet pierces through a plate of mass $M _1=1 kg$ and then comes to rest inside a second plate of mass $M _2=$ $2.98 kg$ as shown in the figure. It is found that the two plates initially at rest, now move with equal velocities. Find the percentage loss in the initial velocity of the bullet when it is between $M _1$ and $M _2$. Neglect any loss of material of the plates due to the action of bullet. Both plates are lying on smooth table.
(1979)
Show Answer
Answer:
Correct Answer: 38. $25 %$
Solution:
- Applying conservation of linear momentum twice. We have
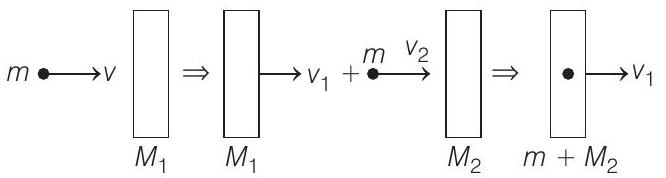
$$ \begin{aligned} & m v=M _1 v _1+m v _2 \\ & m v _2=\left(M _2+m\right) v _1 \end{aligned} $$
Solving Eqs. (i) and (ii), we get
$$ \frac{v _2}{v}=\frac{M _2+m}{M _1+M _2+m} $$
Substituting the values of $m: M _1$ and $M _2$ we get percentage of velocity retained by bullet
$$ \begin{aligned} & \frac{v _2}{v} \times 100 & =\frac{2.98+0.02}{1+2.98+0.02} \times 100=75 % \\ \therefore & \quad % \text { loss } & =25 % \end{aligned} $$






