Centre of Mass 3 Question 3
3. A particle of mass $m$ is moving with speed $2 v$ and collides with a mass $2 m$ moving with speed $v$ in the same direction. After collision, the first mass is stopped completely while the second one splits into two particles each of mass $m$, which move at angle $45^{\circ}$ with respect to the original direction.
The speed of each of the moving particle will be
(2019 Main, 9 April II)
(a) $\sqrt{2} v$
(b) $\frac{v}{\sqrt{2}}$
(c) $\frac{v}{(2 \sqrt{2})}$
(d) $2 \sqrt{2} v$
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- According to the questions,
Initial condition,

Final condition,
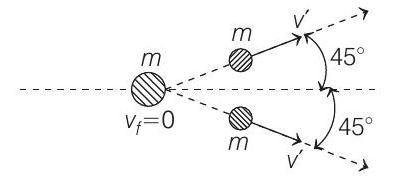
As we know that, in collision, linear momentum is conserved in both $x$ and $y$ directions separately.
So, $\quad\left(p _x\right) _{\text {initial }}=\left(p _x\right) _{\text {final }}$
$m(2 v)+2 m(v)=0+m v^{\prime} \cos 45^{\circ}+m v^{\prime} \cos 45^{\circ}$
$$ \Rightarrow \quad 4 m v=\frac{2 m}{\sqrt{2}} v^{\prime} \Rightarrow v^{\prime}=2 \sqrt{2} v $$
So, each particle will move with a speed of $2 \sqrt{2} v$.






