Centre of Mass 3 Question 3
3. A particle of mass
The speed of each of the moving particle will be
(2019 Main, 9 April II)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- According to the questions,
Initial condition,

Final condition,
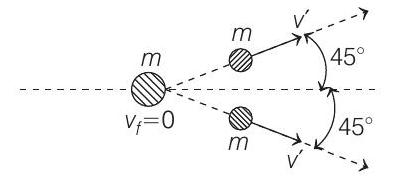
As we know that, in collision, linear momentum is conserved in both
So,
So, each particle will move with a speed of






