SATHEE: Centre of Mass 3 Question 2

Centre of Mass 3 Question 2

2. Two particles of masses $M$ and $2 M$ , moving as shown, with speeds of $10 m / s$ and $5 m / s$ , collide elastically at the origin. After the collision, they move along the indicated directions with speed $v_{1}$ and $v_{2}$ are nearly

(2019 Main, 10 April I)

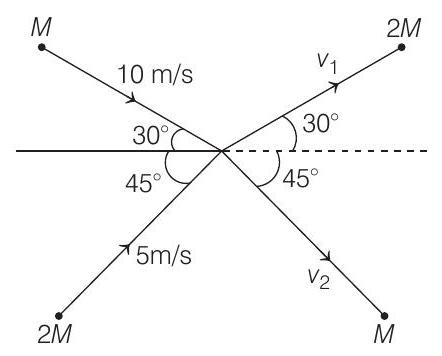
(a) $6.5 m / s$ and $3.2 m / s$

(b) $3.2 m / s$ and $6.3 m / s$

(d) $6.5 m / s$ and $6.3 m / s$

Show Answer

Answer:

Correct Answer: 2. (d)

Solution:

The given condition can be drawn as shown below

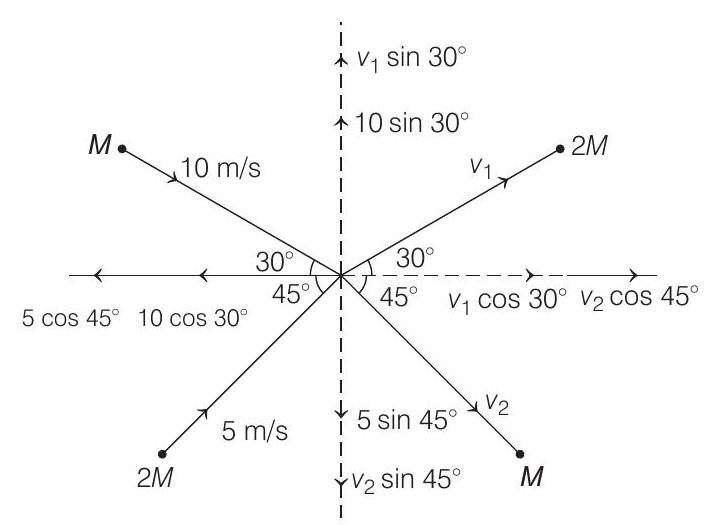
Applying linear momentum conservation law in $x$ -direction, we get

Initial momentum $=$ Final momentum

$\begin{aligned} (M \times 10 \cos 30^{\circ}) + (2 M \times 5 \cos 45^{\circ}) \\ = (M \times v_{2} \cos 45^{\circ}) + (2 M \times v_{1} \cos 30^{\circ}) \\ \Rightarrow M \times 10 \times \frac{\sqrt{3}}{2} + 2 M \times 5 \times \frac{1}{\sqrt{2}} \\ = M \times v_{2} \times \frac{1}{\sqrt{2}} + 2 M \times v_{1} \times \frac{\sqrt{3}}{2} \\ \Rightarrow 5 \sqrt{3} + 5 \sqrt{2} = \frac{v_{2}}{\sqrt{2}} + v_{1} \sqrt{3} \dots (i) \end{aligned}$

Similarly, applying linear momentum conservation law in $y$ -direction, we get

$(M \times 10 \sin 30^{\circ}) - (2 M \times 5 \sin 45^{\circ})$

$= (M \times v_{2} \sin 45^{\circ}) - (2 M \times v_{1} \sin 30^{\circ})$

$\Rightarrow M \times 10 \times \frac{1}{2} - 2 M \times 5 \times \frac{1}{\sqrt{2}}$

$= M \times v_{2} \times \frac{1}{\sqrt{2}} - 2 M \times v_{1} \times \frac{1}{2}$

$\Rightarrow 5 - 5 \sqrt{2} = \frac{v_{2}}{\sqrt{2}} - v_{1}$

Subtracting Eq. (ii) from Eq. (i), we get

$\begin{aligned} (5 \sqrt{3} + 5 \sqrt{2}) - (5 - 5 \sqrt{2}) \\ = \frac{v_{2}}{\sqrt{2}} + v_{1} \sqrt{3} - \frac{v_{2}}{\sqrt{2}} - v_{1} \\ \Rightarrow 5 \sqrt{3} + 10 \sqrt{2} - 5 = v_{1} \sqrt{3} + v_{1} \\ \Rightarrow v_{1} = \frac{5 \sqrt{3} + 10 \sqrt{2} - 5}{1 + \sqrt{3}} = \frac{8.66 + 14.142 - 5}{1 + 1.732} \\ = \frac{17.802}{2.732} \Rightarrow v_{1} = 6.516 m / s \approx 6.5 m / s \\ … (iii) \end{aligned}$

Substituting the value from Eq. (iii) in Eq. (i), we get

$\begin{aligned} 5 \sqrt{3} + 5 \sqrt{2} & = \frac{v_{2}}{\sqrt{2}} + 6.51 \times \sqrt{3} \\ \Rightarrow & v_{2} & = (5 \sqrt{3} + 5 \sqrt{2} - 6.51 \times \sqrt{3}) \sqrt{2} \\ v_{2} & = (8.66 + 7.071 - 11.215) 1.414 \\ \Rightarrow & v_{2} & = 4.456 \times 1.414 \\ v_{2} & \approx 6.3 m / s \end{aligned}$

Centre of Mass 3 Question 2

2. Two particles of masses $M$ and $2 M$ , moving as shown, with speeds of $10 m / s$ and $5 m / s$ , collide elastically at the origin. After the collision, they move along the indicated directions with speed $v_{1}$ and $v_{2}$ are nearly

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Centre of Mass 3 Question 2

2. Two particles of masses M and 2M, moving as shown, with speeds of 10m/s and 5m/s, collide elastically at the origin. After the collision, they move along the indicated directions with speed v1 and v2 are nearly

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu

2. Two particles of masses $M$ and $2 M$ , moving as shown, with speeds of $10 m / s$ and $5 m / s$ , collide elastically at the origin. After the collision, they move along the indicated directions with speed $v_{1}$ and $v_{2}$ are nearly