Centre of Mass 2 Question 9
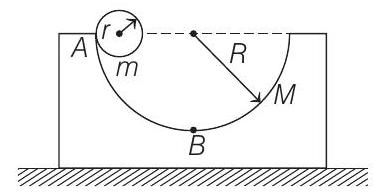
10. A block of mass $M$ with a semicircular track of radius $R$, rests on a horizontal frictionless surface. A uniform cylinder of radius $r$ and mass $m$ is released from rest at the top point $A$ (see fig.). The cylinder slips on the semicircular frictionless track.
(a) How far has the block moved when the cylinder reaches the bottom (point $B$ ) of the track ?
(b) How fast is the block moving when the cylinder reaches the bottom of the track?
$(1983,7$ M)
Show Answer
Answer:
Correct Answer: 10. $\frac{m(R-r)}{M+m}, m \sqrt{\frac{2 g(R-r)}{M(M+m)}}$
Solution:
- (a) The centre of mass of $M+m$ in this case will not move in horizontal direction. Let $M$ moves towards left by a distance $x$ then $m$ will move towards right by a distance $R-r-x$ (with respect to ground). For centre of mass not to move along horizontal we should have
$$ M x=m(R-r-x), \quad x=\frac{m(R-r)}{M+m} $$
(b) Let $v _1$ be the speed of $m$ towards right and $v _2$ the speed of $M$ towards left. From conservation of linear momentum.
$$ m v _1=M v _2 \ldots(i) $$
From conservation of mechanical energy
$$ m g(R-r)=\frac{1}{2} m v _1^{2}+\frac{1}{2} M v _2^{2} $$
Solving these two equations, we get
$$ v _2=m \sqrt{\frac{2 g(R-r)}{M(M+m)}} $$
