Centre of Mass 2 Question 9
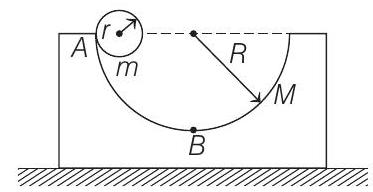
10. A block of mass
(a) How far has the block moved when the cylinder reaches the bottom (point
(b) How fast is the block moving when the cylinder reaches the bottom of the track?
Show Answer
Answer:
Correct Answer: 10.
Solution:
- (a) The centre of mass of
(b) Let
From conservation of mechanical energy
Solving these two equations, we get






