Centre of Mass 2 Question 8
9. Two bodies $A$ and $B$ of masses $m$ and $2 m$ respectively are placed on a smooth floor. They are connected by a spring. A third body $C$ of mass $m$ moves with velocity $v _0$ along the line joining $A$ and $B$ and collides elastically with $A$ as shown in figure. At a certain instant of time $t _0$ after collision, it is found that the instantaneous velocities of $A$ and $B$ are the same. Further at this instant the compression of the spring is found to be $x _0$. Determine (a) the common velocity of $A$ and $B$ at time $t _0$ and (b) the spring constant.
$(1984,6 M)$
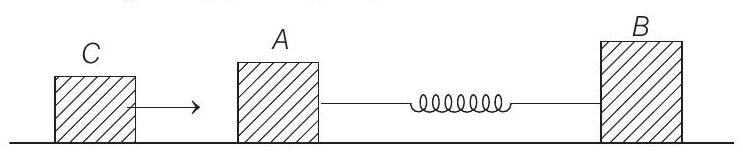
Show Answer
Answer:
Correct Answer: 9. (a) $\frac{v _0}{3}$
(b) $\frac{2 m v _0^{2}}{3 x _0^{2}}$
Solution:
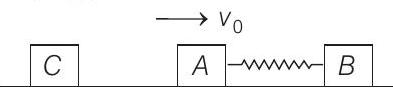
- (a) Collision between $A$ and $C$ is elastic and mass of both the blocks is same. Therefore, they will exchange their velocities i.e. $C$ will come to rest and $A$ will be moving will velocity $v _0$. Let $v$ be the common velocity of $A$ and $B$, then from conservation of linear momentum, we have
(a)

$B$
At rest
(b)
(c)
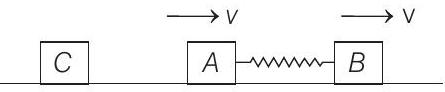
$m _A v _0=\left(m _A+m _B\right) v$ or $m v _0=(m+2 m) v$ or $v=\frac{v _0}{3}$
(b) From conservation of energy, we have
$$ \begin{aligned} & \frac{1}{2} m _A v _0^{2}=\frac{1}{2}\left(m _A+m _B\right) v^{2}+\frac{1}{2} k x _0^{2} \\ & \text { or } \\ & \frac{1}{2} m v _0^{2}=\frac{1}{2}(3 m){\frac{v _0}{3}}^{2}+\frac{1}{2} k x _0^{2} \\ & \text { or } \quad \frac{1}{2} k x _0^{2}=\frac{1}{3} m v _0^{2} \quad \text { or } k=\frac{2 m v _0^{2}}{3 x _0^{2}} \end{aligned} $$






