Centre of Mass 2 Question 8
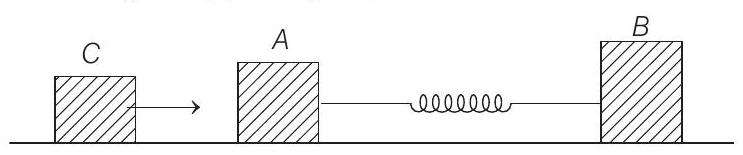
9. Two bodies
Show Answer
Answer:
Correct Answer: 9. (a)
(b)
Solution:
- (a) Collision between
(a)

At rest
(b)
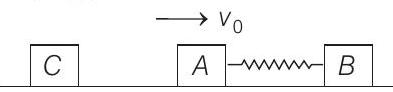
(c)
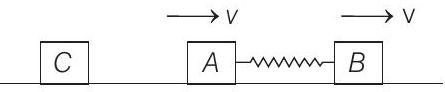
(b) From conservation of energy, we have






