Centre of Mass 2 Question 7
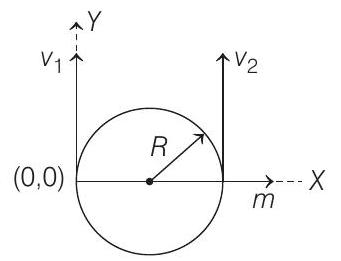
8. A particle of mass $m$, moving in a circular path of radius $R$ with a constant speed $v _2$ is located at point $(2 R, 0)$ at time $t=0$ and a man starts moving with a velocity $v _1$ along the positive $Y$-axis from origin at time $t=0$. Calculate the linear momentum of the particle w.r.t. man as a function of time.
$(2003,2 M)$
Show Answer
Answer:
Correct Answer: 8. $-m v _2 \sin \frac{v _2}{R} t \hat{\mathbf{i}}+m \quad v _2 \cos \frac{v _2}{R} t-v _1 \hat{\mathbf{j}}$
Solution:
- Angular speed of particle about centre of the circle
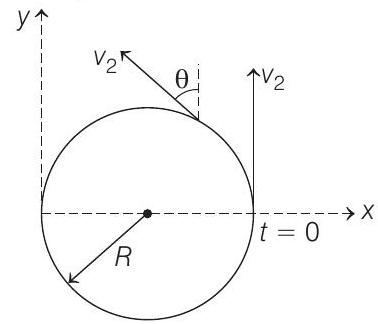
$$ \omega=\frac{v _2}{R}, \theta=\omega t=\frac{v _2}{R} t $$
$\mathbf{v} _p=\left(-v _2 \sin \theta \hat{\mathbf{i}}+v _2 \cos \theta \hat{\mathbf{j}}\right)$
or $\quad \mathbf{v} _p=-v _2 \sin \frac{v _2}{R} t \hat{\mathbf{i}}+v _2 \cos \frac{v _2}{R} t \hat{\mathbf{j}}$
and
$$ \mathbf{v} _m=v _1 \hat{\mathbf{j}} $$
$\therefore$ Linear momentum of particle w.r.t. man as a function of time is
$$ \begin{aligned} \mathbf{L} _{p m}=m & \left(\mathbf{v} _p-\mathbf{v} _m\right) \\ & =m-v _2 \sin \frac{v _2}{R} t \hat{\mathbf{i}}+v _2 \cos \frac{v _2}{R} t-v _1 \hat{\mathbf{j}} \end{aligned} $$






