Centre of Mass 2 Question 7
8. A particle of mass
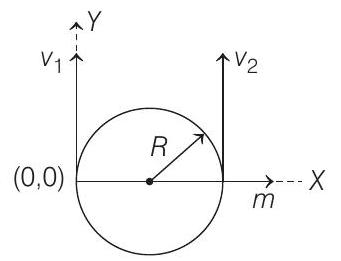
Show Answer
Answer:
Correct Answer: 8.
Solution:
- Angular speed of particle about centre of the circle
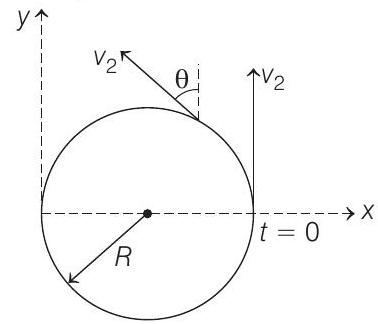
or
and






