Centre of Mass 1 Question 2
2. A uniform rectangular thin sheet $A B C D$ of mass $M$ has length $a$ and breadth $b$, as shown in the figure. If the shaded portion $H B G O$ is cut-off, the coordinates of the centre of mass of the remaining portion will be
(2019 Main, 8 April II)
(a) $\frac{2 a}{3}, \frac{2 b}{3}$
(b) $\frac{5 a}{12}, \frac{5 b}{12}$
(c) $\frac{3 a}{4}, \frac{3 b}{4}$
(d) $\frac{5 a}{3}, \frac{5 b}{3}$
Show Answer
Answer:
Correct Answer: 2. (b)
Solution:
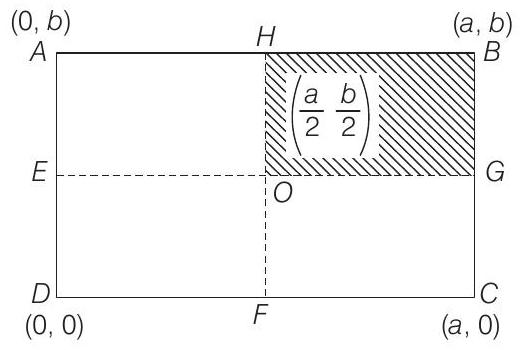
- The given rectangular thin sheet $A B C D$ can be drawn as shown in the figure below,
Here,
Area of complete lamina, $A _1=a b$
Area of shaded part of lamina $=\frac{a}{2} \times \frac{b}{2}=\frac{a b}{4}$
$\left(x _1, y _1\right)=$ coordinates of centre of mass of complete lamina
$$ =\frac{a}{2}, \frac{a}{2} $$
$\left(x _2, y _2\right)=$ coordinates of centre of mass of shaded part of lamina $=\frac{3 a}{4}, \frac{3 a}{4}$
$\therefore$ Using formula for centre of mass, we have
$X _{CM}=\frac{A _1 x _1-A _2 x _2}{A _1-A _2}$
$$ =\frac{a b \frac{a}{2}-\frac{a b}{4} \frac{3 a}{4}}{a b-\frac{a b}{4}}=\frac{\frac{8 a^{2} b-3 a^{2} b}{16}}{\frac{3 a b}{4}}=\frac{5 a}{12} $$
Similarly, $Y _{CM}=\frac{A _1 y _1-A _2 y _2}{A _1-A _2}$
$$ =\frac{a b \frac{b}{2}-\frac{a b}{4} \frac{3 b}{4}}{a b-\frac{a b}{4}}=\frac{5 b}{12} $$
The coordinate of the centre of mass is $\frac{5 a}{12}, \frac{5 b}{12}$.
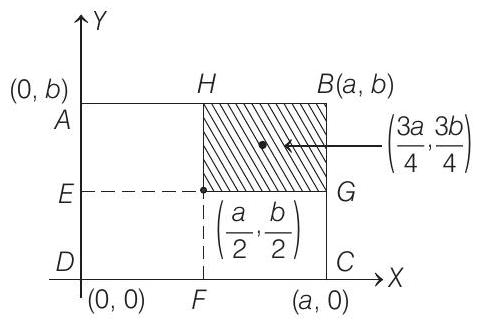
Alternate Solution
Let $m$ be the mass of entire rectangular lamina.
So, the mass of the shaded portion of lamina $=\frac{m}{4}$
Using the relation,
$$ \begin{aligned} X _{CM} & =\frac{m _1 x _1-m _2 x _2}{m _1-m _2}, \text { we get } \\ X _{CM} & =\frac{m \frac{a}{2}-\frac{m}{4} \frac{3 a}{4}}{m-\frac{m}{4}}=\frac{\frac{a}{2}-\frac{3 a}{16}}{\frac{3}{4}}=\frac{5 a}{12} \end{aligned} $$
Similarly, $Y _{CM}=\frac{m _1 y _1-m _2 y _2}{m _1-m _2}$, we get
$$ Y _{CM}=\frac{m \frac{a}{2}-\frac{m}{4} \frac{3 b}{4}}{m-\frac{m}{4}}=\frac{\frac{b}{2}-\frac{3 b}{16}}{\frac{3}{4}}=\frac{5 b}{12} $$
$\therefore$ The coordinates of the centre of mass of remaining portion will be $\frac{5 a}{12}, \frac{5 b}{12}$.
