Centre of Mass 1 Question 2
2. A uniform rectangular thin sheet
(2019 Main, 8 April II)
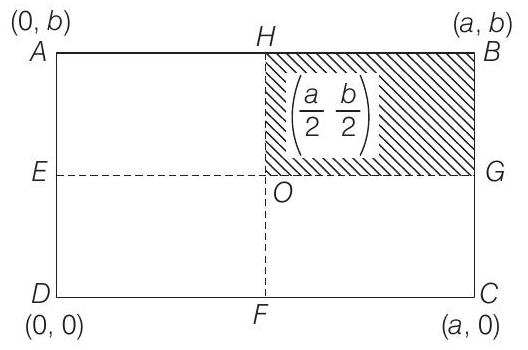
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 2. (b)
Solution:
- The given rectangular thin sheet
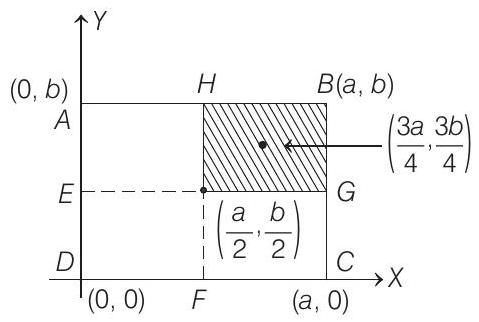
Here,
Area of complete lamina,
Area of shaded part of lamina
Similarly,
The coordinate of the centre of mass is
Alternate Solution
Let
So, the mass of the shaded portion of lamina
Using the relation,
Similarly,






