Centre of Mass 1 Question 1
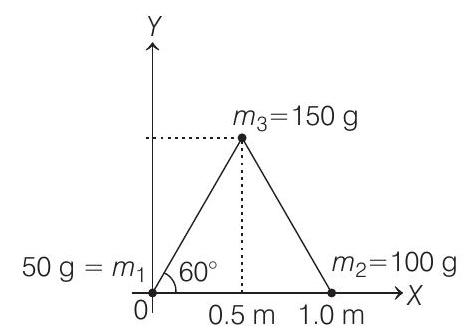
1. Three particles of masses $50 g, 100 g$ and $150 g$ are placed at the vertices of an equilateral triangle of side $1 m$ (as shown in the figure). The $(x, y)$ coordinates of the centre of mass will be
(2019 Main, 12 April II)
(a) $\frac{\sqrt{3}}{4} m, \frac{5}{12} m$
(b) $\frac{7}{12} m, \frac{\sqrt{3}}{8} m$
(c) $\frac{7}{12} m, \frac{\sqrt{3}}{4} m$
(d) $\frac{\sqrt{3}}{8} m, \frac{7}{12} m$
Show Answer
Answer:
Correct Answer: 1. (c)
Solution:
- The height of equilateral $\Delta$ is
$h=y _3=\sqrt{(1)^{2}-(0.5)^{2}}=\sqrt{3} / 2 m$
Thus, coordinates of three masses are $(0,0),(1,0)$
and $0.5, \frac{\sqrt{3}}{2}$
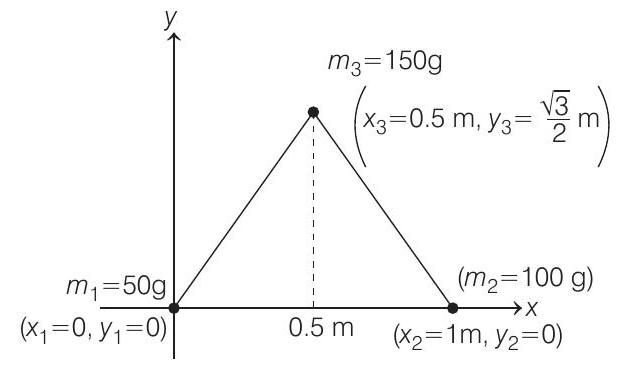
Using, $\quad X _{CM}=\frac{m _1 x _1+m _2 x _2+m _3 x _3}{m _1+m _2+m _3}$
we have
$$ \begin{aligned} X _{CM} & =\frac{50 \times 0+100 \times 1+150 \times 0.5}{50+100+150} \\ & =\frac{175}{300}=\frac{7}{12} m \end{aligned} $$
Similarly,
$$ \begin{aligned} Y _{CM} & =\frac{m _1 y _1+m _2 y _2+m _3 y _3}{m _1+m _2+m _3} \\ & =\frac{50 \times 0+100 \times 0+150 \times \frac{\sqrt{3}}{2}}{50+100+150} \\ & =\frac{\sqrt{3}}{4} m \end{aligned} $$






