Centre of Mass 1 Question 1
1. Three particles of masses
(2019 Main, 12 April II)
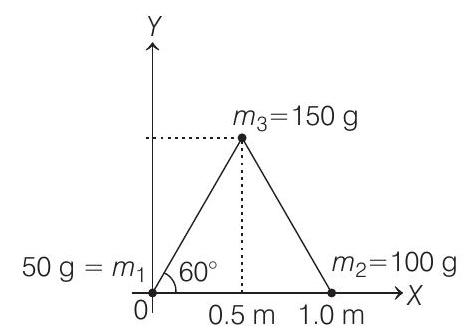
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 1. (c)
Solution:
- The height of equilateral
Thus, coordinates of three masses are
and
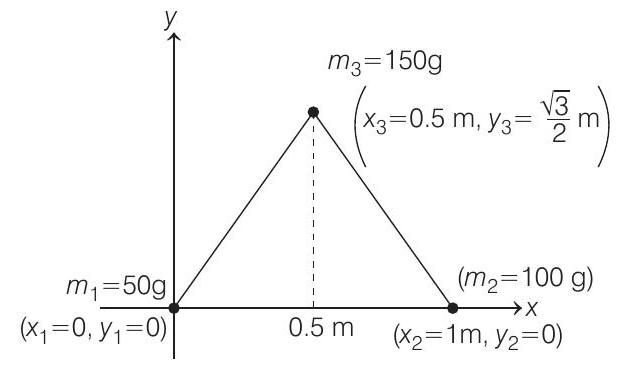
Using,
we have
Similarly,






