SATHEE: Vectors 5 Question 11

Vectors 5 Question 11

11. The position vectors of the vertices $A, B$ and $C$ of a tetrahedron $A B C D$ are $\hat{i} + \hat{j} + \hat{k}, \hat{i}$ and $3 \hat{i}$ , respectively. The altitude from vertex $D$ to the opposite face $A B C$ meets the median line through $A$ of the $△ A B C$ at a point $E$ . If the length of the side $A D$ is 4 and the volume of the tetrahedron is $\frac{2 \sqrt{2}}{3}$ , then find the position vector of the point $E$ for all its possible positions.

(1996, 5M)

Show Answer

Answer:

Correct Answer: 11. $- \hat{i} - 8 \hat{j} + 2 \hat{k}$ 16. $0, - 1$

Solution:

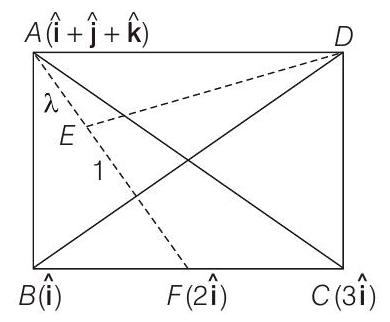
$F$ is mid-point of $B C$ i.e. $F = \frac{\hat{i} + 3 \hat{i}}{2} = 2 \hat{i}$ and $A E ⊥ D E$

[given]

Let $E$ divides $A F$ in $λ : 1$ . The position vector of $E$ is given by

$\frac{2 λ \hat{i} + 1 (\hat{i} + \hat{j} + \hat{k})}{λ + 1} = (\frac{2 λ + 1}{λ + 1}) \hat{i} + \frac{1}{λ + 1} \hat{j} + \frac{1}{λ + 1} \hat{k}$

Now, volume of the tetrahedron

$\begin{aligned} = \frac{1}{3} (area of the base) (height) \\ \Rightarrow \frac{2 \sqrt{2}}{3} & = \frac{1}{3} (area of the △ A B C) (D E) \end{aligned}$

But area of the $△ A B C = \frac{1}{2} | \vec{B C} \times \vec{B A} |$

$\begin{aligned} = \frac{1}{2} | 2 \hat{i} \times (\hat{j} + \hat{k}) | & = | \hat{i} \times \hat{j} + \hat{i} \times \hat{k} | & = | \hat{k} - \hat{j} | = \sqrt{2} \\ ∴ & \frac{2 \sqrt{2}}{3} & = \frac{1}{3} (\sqrt{2}) (D E) \Rightarrow D E = 2 \end{aligned}$

Since, $△ A D E$ is a right angle triangle, then

$\begin{aligned} A D^{2} = A E^{2} + D E^{2} \\ \Rightarrow (4)^{2} = A E^{2} + (2)^{2} \Rightarrow A E^{2} = 12 \\ But \vec{A E} = \frac{2 λ + 1}{λ + 1} \hat{i} + \frac{1}{λ + 1} \hat{j} + \frac{1}{λ + 1} \hat{k} - (\hat{i} + \hat{j} + \hat{k}) \\ = \frac{λ}{λ + 1} \hat{i} - \frac{λ}{λ + 1} \hat{j} - \frac{λ}{λ + 1} \hat{k} \\ \Rightarrow | \vec{A E} |^{2} = \frac{1}{(λ + 1)^{2}} [λ^{2} + λ^{2} + λ^{2}] = \frac{3 λ^{2}}{(λ + 1)^{2}} \end{aligned}$

Therefore, $12 = \frac{3 λ^{2}}{(λ + 1)^{2}}$

$\begin{aligned} \Rightarrow 4 (λ + 1)^{2} = λ^{2} \Rightarrow 4 λ^{2} + 4 + 8 λ = λ^{2} \\ \Rightarrow 3 λ^{2} + 8 λ + 4 = 0 \Rightarrow 3 λ^{2} + 6 λ + 2 λ + 4 = 0 \\ \Rightarrow 3 λ (λ + 2) + 2 (λ + 2) = 0 \\ \Rightarrow (3 λ + 2) (λ + 2) = 0 \Rightarrow λ = - 2 / 3, λ = - 2 \end{aligned}$

When $λ = - 2 / 3$ , position vector of $E$ is given by

$\begin{aligned} (\frac{2 λ}{λ + 1} + 1) \hat{i} + \frac{1}{λ + 1} \hat{j} + \frac{1}{λ + 1} \hat{k} \\ = \frac{2 \cdot (- 2 / 3) + 1}{- 2 / 3 + 1} \hat{i} + \frac{1}{- 2 / 3 + 1} \hat{j} + \frac{1}{- 2 / 3 + 1} \hat{k} \\ = \frac{- 4 / 3 + 1}{\frac{- 2 + 3}{3}} \hat{i} + \frac{1}{\frac{- 2 + 3}{3}} \hat{j} + \frac{1}{\frac{- 2 + 3}{3}} \hat{k} \\ = \frac{- 4 + 3}{1 / 3} \hat{i} + \frac{1}{1 / 3} \hat{j} + \frac{1}{1 / 3} \hat{k} = - \hat{i} + 3 \hat{j} + 3 \hat{k} \end{aligned}$

and when $λ = - 2$ , position vector of $E$ is given by,

$\begin{array}{r} \frac{2 \times (- 2) + 1}{- 2 + 1} \hat{i} + \frac{1}{- 2 + 1} \hat{j} + \frac{1}{- 2 + 1} \hat{k} = \frac{- 4 + 1}{- 1} \hat{i} - \hat{j} - \hat{k} \\ = 3 \hat{i} - \hat{j} - \hat{k} \end{array}$

Therefore, $- \hat{i} + 3 \hat{j} + 3 \hat{k}$ and $+ 3 \hat{i} - \hat{j} - \hat{k}$ are the answer.

Vectors 5 Question 11

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Vectors 5 Question 11

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu