Vectors 5 Question 11
11. The position vectors of the vertices $A, B$ and $C$ of a tetrahedron $A B C D$ are $\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}, \hat{\mathbf{i}}$ and $3 \hat{\mathbf{i}}$, respectively. The altitude from vertex $D$ to the opposite face $A B C$ meets the median line through $A$ of the $\triangle A B C$ at a point $E$. If the length of the side $A D$ is 4 and the volume of the tetrahedron is $\frac{2 \sqrt{2}}{3}$, then find the position vector of the point $E$ for all its possible positions.
(1996, 5M)
Show Answer
Answer:
Correct Answer: 11. $-\hat{\mathbf{i}}-8 \hat{\mathbf{j}}+2 \hat{\mathbf{k}} \quad$ 16. $0,-1$
Solution:
- $F$ is mid-point of $B C$ i.e. $F=\frac{\hat{\mathbf{i}}+3 \hat{\mathbf{i}}}{2}=2 \hat{\mathbf{i}}$ and $A E \perp D E$
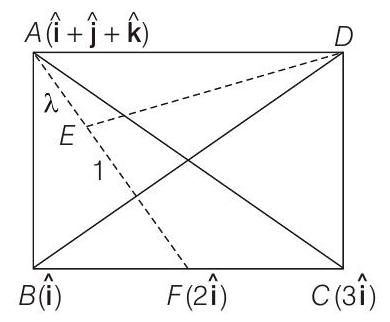
[given]
Let $E$ divides $A F$ in $\lambda: 1$. The position vector of $E$ is given by
$$ \frac{2 \lambda \hat{\mathbf{i}}+1(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}})}{\lambda+1}=\left(\frac{2 \lambda+1}{\lambda+1}\right) \hat{\mathbf{i}}+\frac{1}{\lambda+1} \hat{\mathbf{j}}+\frac{1}{\lambda+1} \hat{\mathbf{k}} $$
Now, volume of the tetrahedron
$$ \begin{aligned} & =\frac{1}{3}(\text { area of the base) (height) } \\ \Rightarrow \quad \frac{2 \sqrt{2}}{3} & =\frac{1}{3}(\text { area of the } \triangle A B C)(D E) \end{aligned} $$
But area of the $\triangle A B C=\frac{1}{2}|\overrightarrow{\mathbf{B C}} \times \overrightarrow{\mathbf{B A}}|$
$$ \begin{array}{rlrl} & =\frac{1}{2}|2 \hat{\mathbf{i}} \times(\hat{\mathbf{j}}+\hat{\mathbf{k}})| & =|\hat{\mathbf{i}} \times \hat{\mathbf{j}}+\hat{\mathbf{i}} \times \hat{\mathbf{k}}| & =|\hat{\mathbf{k}}-\hat{\mathbf{j}}|=\sqrt{2} \\ \therefore & \frac{2 \sqrt{2}}{3} & =\frac{1}{3}(\sqrt{2})(D E) \Rightarrow D E=2 \end{array} $$
Since, $\triangle A D E$ is a right angle triangle, then
$$ \begin{aligned} & A D^{2}=A E^{2}+D E^{2} \\ & \Rightarrow \quad(4)^{2}=A E^{2}+(2)^{2} \Rightarrow A E^{2}=12 \\ & \text { But } \quad \overrightarrow{\mathbf{A E}}=\frac{2 \lambda+1}{\lambda+1} \hat{\mathbf{i}}+\frac{1}{\lambda+1} \hat{\mathbf{j}}+\frac{1}{\lambda+1} \hat{\mathbf{k}}-(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}) \\ & =\frac{\lambda}{\lambda+1} \hat{\mathbf{i}}-\frac{\lambda}{\lambda+1} \hat{\mathbf{j}}-\frac{\lambda}{\lambda+1} \hat{\mathbf{k}} \\ & \Rightarrow \quad|\overrightarrow{\mathbf{A E}}|^{2}=\frac{1}{(\lambda+1)^{2}}\left[\lambda^{2}+\lambda^{2}+\lambda^{2}\right]=\frac{3 \lambda^{2}}{(\lambda+1)^{2}} \end{aligned} $$
Therefore, $12=\frac{3 \lambda^{2}}{(\lambda+1)^{2}}$
$$ \begin{aligned} & \Rightarrow \quad 4(\lambda+1)^{2}=\lambda^{2} \Rightarrow 4 \lambda^{2}+4+8 \lambda=\lambda^{2} \\ & \Rightarrow \quad 3 \lambda^{2}+8 \lambda+4=0 \Rightarrow 3 \lambda^{2}+6 \lambda+2 \lambda+4=0 \\ & \Rightarrow 3 \lambda(\lambda+2)+2(\lambda+2)=0 \\ & \Rightarrow \quad(3 \lambda+2)(\lambda+2)=0 \Rightarrow \lambda=-2 / 3, \lambda=-2 \end{aligned} $$
When $\lambda=-2 / 3$, position vector of $E$ is given by
$$ \begin{aligned} &\left(\frac{2 \lambda}{\lambda+1}+1\right) \hat{\mathbf{i}}+\frac{1}{\lambda+1} \hat{\mathbf{j}}+\frac{1}{\lambda+1} \hat{\mathbf{k}} \\ &=\frac{2 \cdot(-2 / 3)+1}{-2 / 3+1} \hat{\mathbf{i}}+\frac{1}{-2 / 3+1} \hat{\mathbf{j}}+\frac{1}{-2 / 3+1} \hat{\mathbf{k}} \\ & \quad=\frac{-4 / 3+1}{\frac{-2+3}{3}} \hat{\mathbf{i}}+\frac{1}{\frac{-2+3}{3}} \hat{\mathbf{j}}+\frac{1}{\frac{-2+3}{3}} \hat{\mathbf{k}} \\ & \quad= \frac{-4+3}{1 / 3} \hat{\mathbf{i}}+\frac{1}{1 / 3} \hat{\mathbf{j}}+\frac{1}{1 / 3} \hat{\mathbf{k}}=-\hat{\mathbf{i}}+3 \hat{\mathbf{j}}+3 \hat{\mathbf{k}} \end{aligned} $$
and when $\lambda=-2$, position vector of $E$ is given by,
$$ \begin{array}{r} \frac{2 \times(-2)+1}{-2+1} \hat{\mathbf{i}}+\frac{1}{-2+1} \hat{\mathbf{j}}+\frac{1}{-2+1} \hat{\mathbf{k}}=\frac{-4+1}{-1} \hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}} \\ =3 \hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}} \end{array} $$
Therefore, $-\hat{\mathbf{i}}+3 \hat{\mathbf{j}}+3 \hat{\mathbf{k}}$ and $+3 \hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}}$ are the answer.
