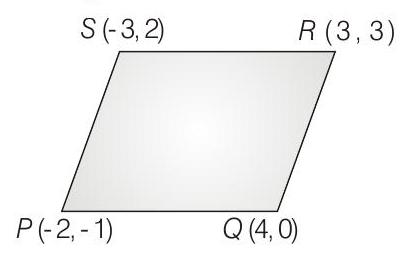
Vectors 1 Question 8
9. Let
(2010)
(a) parallelogram, which is neither a rhombus nor a rectangle
(b) square
(c) rectangle, but not a square
(d) rhombus, but not a square
Show Answer
Answer:
Correct Answer: 9. (a)
Solution: