Vectors 1 Question 8
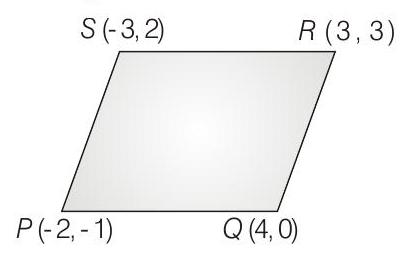
9. Let $P, Q, R$ and $S$ be the points on the plane with position vectors $-2 \hat{i}-\hat{j}, 4 \hat{i}, 3 \hat{i}+3 \hat{j}$ and $-3 \hat{i}+2 \hat{j}$, respectively. The quadrilateral $P Q R S$ must be a
(2010)
(a) parallelogram, which is neither a rhombus nor a rectangle
(b) square
(c) rectangle, but not a square
(d) rhombus, but not a square
Show Answer
Answer:
Correct Answer: 9. $\left(\frac{\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}}{|\overrightarrow{\mathbf{b}}|^{2}}\right) \overrightarrow{\mathbf{b}}$ and $\overrightarrow{\mathbf{a}}-\left(\frac{\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}}{|\overrightarrow{\mathbf{b}}|^{2}}\right) \overrightarrow{\mathbf{b}}$
Solution:
- $m _{P Q}=\frac{1}{6}, m _{S R}=\frac{1}{6}, m _{R Q}=-3, m _{S P}=-3$
$\Rightarrow$ Parallelogram, but neither $P R=S Q$ nor $P R \perp S Q$.
$\therefore$ So, it is a parallelogram, which is neither a rhombus nor a rectangle.
