SATHEE: Vectors 1 Question 26

Vectors 1 Question 26

27. In a $△ A B C, D$ and $E$ are points on $B C$ and $A C$ respectively, such that $B D = 2 D C$ and $A E = 3 E C$ . Let $P$ be the point of intersection of $A D$ and $B E$ . Find $B P / P E$ using vector methods.

(1993, 5M)

Show Answer

Answer:

Correct Answer: 27. $(a, c)$

Solution:

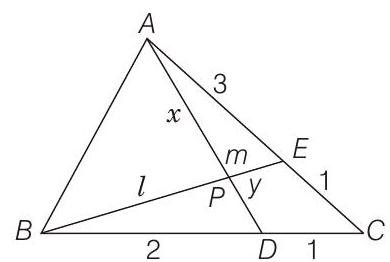
Let the position vectors of $A, B$ and $C$ are $\vec{a}, \vec{b}$ and $\vec{c}$ respectively, since the point $D$ divides $B C$ in the ratio of $2 : 1$ , the position vector of $D$ will be

$D \equiv (\frac{2 \vec{c} + \vec{b}}{3})$

and the point $E$ divides $A C$ in the ratio $3 : 1$ ,

therefore $E \equiv (\frac{3 \vec{c} + \vec{a}}{4})$ .

Now, let $P$ divides $B E$ in the ratio $l : m$ and $A D$ in the ratio $x : y$ .

Hence, the position vector of $P$ getting from $B E$ and $A D$ must be the same.

Hence, we have

$\begin{aligned} \frac{l (\frac{3 \vec{c} + \vec{a}}{4}) + m \vec{b}}{l + m} = \frac{x (\frac{2 \vec{c} + \vec{b}}{3}) + y \vec{a}}{x + y} \\ \Rightarrow \frac{\frac{3 l \vec{c}}{4} + \frac{l \vec{a}}{4} + m \vec{b}}{l + m} = \frac{\frac{2 \vec{c} x}{3} + \frac{\vec{b} x}{3} + y \vec{a}}{x + y} \\ \Rightarrow \frac{3 l}{4 (l + m)} \vec{c} + \frac{l}{4 (l + m)} \vec{a} + \frac{m \vec{b}}{l + m} \\ = \frac{2 x}{3 (x + y)} \vec{c} + \frac{x}{3 (x + y)} \vec{b} + \frac{y}{(x + y)} \vec{a} \end{aligned}$

Now, comparing the coefficients, we get

$\begin{aligned} \frac{3 l}{4 (l + m)} & = \frac{2 x}{3 (x + y)} \\ \frac{l}{4 (l + m)} & = \frac{y}{x + y}, \\ \frac{m}{l + m} & = \frac{x}{3 (x + y)} \end{aligned}$

On dividing Eq. (i) by Eq. (iii), we get

$\begin{matrix} \frac{\frac{3 l}{4 (l + m)}}{\frac{m}{l + m}} = \frac{\frac{2 x}{3 (x + y)}}{\frac{x}{3 (x + y)}} \\ \Rightarrow \frac{3}{4} \cdot \frac{l}{m} = 2 \Rightarrow \frac{l}{m} = \frac{8}{3} = \frac{B P}{P E} \end{matrix}$

Vectors 1 Question 26

27. In a $△ A B C, D$ and $E$ are points on $B C$ and $A C$ respectively, such that $B D = 2 D C$ and $A E = 3 E C$ . Let $P$ be the point of intersection of $A D$ and $B E$ . Find $B P / P E$ using vector methods.

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Vectors 1 Question 26

27. In a △ABC,D and E are points on BC and AC respectively, such that BD=2DC and AE=3EC. Let P be the point of intersection of AD and BE. Find BP/PE using vector methods.

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu

27. In a $△ A B C, D$ and $E$ are points on $B C$ and $A C$ respectively, such that $B D = 2 D C$ and $A E = 3 E C$ . Let $P$ be the point of intersection of $A D$ and $B E$ . Find $B P / P E$ using vector methods.