Vectors 1 Question 26
27. In a $\triangle A B C, D$ and $E$ are points on $B C$ and $A C$ respectively, such that $B D=2 D C$ and $A E=3 E C$. Let $P$ be the point of intersection of $A D$ and $B E$. Find $B P / P E$ using vector methods.
(1993, 5M)
Show Answer
Answer:
Correct Answer: 27. $(a, c)$
Solution:
- Let the position vectors of $A, B$ and $C$ are $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}$ and $\overrightarrow{\mathbf{c}}$ respectively, since the point $D$ divides $B C$ in the ratio of $2: 1$, the position vector of $D$ will be
$$ D \equiv\left(\frac{2 \overrightarrow{\mathbf{c}}+\overrightarrow{\mathbf{b}}}{3}\right) $$
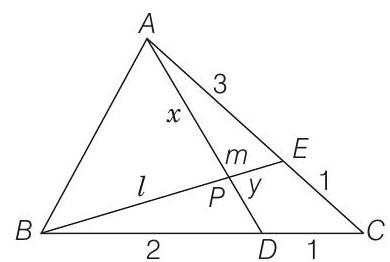
and the point $E$ divides $A C$ in the ratio $3: 1$,
therefore $E \equiv\left(\frac{3 \overrightarrow{\mathbf{c}}+\overrightarrow{\mathbf{a}}}{4}\right)$.
Now, let $P$ divides $B E$ in the ratio $l: m$ and $A D$ in the ratio $x: y$.
Hence, the position vector of $P$ getting from $B E$ and $A D$ must be the same.
Hence, we have
$$ \begin{aligned} & \frac{l\left(\frac{3 \overrightarrow{\mathbf{c}}+\overrightarrow{\mathbf{a}}}{4}\right)+m \overrightarrow{\mathbf{b}}}{l+m}=\frac{x\left(\frac{2 \overrightarrow{\mathbf{c}}+\overrightarrow{\mathbf{b}}}{3}\right)+y \overrightarrow{\mathbf{a}}}{x+y} \\ & \Rightarrow \quad \frac{\frac{3 l \overrightarrow{\mathbf{c}}}{4}+\frac{l \overrightarrow{\mathbf{a}}}{4}+m \overrightarrow{\mathbf{b}}}{l+m}=\frac{\frac{2 \overrightarrow{\mathbf{c}} x}{3}+\frac{\overrightarrow{\mathbf{b}} x}{3}+y \overrightarrow{\mathbf{a}}}{x+y} \\ & \Rightarrow \quad \frac{3 l}{4(l+m)} \overrightarrow{\mathbf{c}}+\frac{l}{4(l+m)} \overrightarrow{\mathbf{a}}+\frac{m \overrightarrow{\mathbf{b}}}{l+m} \\ &=\frac{2 x}{3(x+y)} \overrightarrow{\mathbf{c}}+\frac{x}{3(x+y)} \overrightarrow{\mathbf{b}}+\frac{y}{(x+y)} \overrightarrow{\mathbf{a}} \end{aligned} $$
Now, comparing the coefficients, we get
$$ \begin{aligned} \frac{3 l}{4(l+m)} & =\frac{2 x}{3(x+y)} \\ \frac{l}{4(l+m)} & =\frac{y}{x+y}, \\ \frac{m}{l+m} & =\frac{x}{3(x+y)} \end{aligned} $$
On dividing Eq. (i) by Eq. (iii), we get
$$ \begin{gathered} \frac{\frac{3 l}{4(l+m)}}{\frac{m}{l+m}}=\frac{\frac{2 x}{3(x+y)}}{\frac{x}{3(x+y)}} \\ \Rightarrow \quad \frac{3}{4} \cdot \frac{l}{m}=2 \Rightarrow \frac{l}{m}=\frac{8}{3}=\frac{B P}{P E} \end{gathered} $$
