Theory of Equations 4 Question 2
2. Consider the quadratic equation,
(2019 Main, 10 Jan I)
(a) 11
(b) 10
(c) 12
(d) 18
Show Answer
Answer:
Correct Answer: 2. (a)
Solution:
- Let
Then, according to problem, the graph of 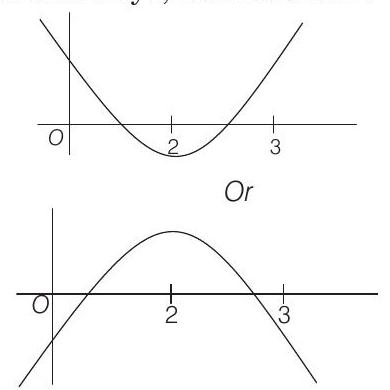
In both cases
Now, consider
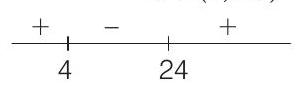
Similarly,
$ \begin{aligned} & {[9(c-5)-6 c+(c-4)]<0} \ & \Rightarrow \quad(c-24)(4 c-49)<0 \ & \begin{array}{lll}
- & - & + \ \hline 49 / 4 & 24 \end{array} \ & \Rightarrow \quad c \in \frac{49}{4}, 24 \end{aligned} $
From Eqs. (i) and (ii), we get






