Theory of Equations 4 Question 2
2. Consider the quadratic equation, $(c-5) x^{2}-2 c x+(c-4)$ $=0, c \neq 5$. Let $S$ be the set of all integral values of $c$ for which one root of the equation lies in the interval $(0,2)$ and its other root lies in the interval $(2,3)$. Then, the number of elements in $S$ is
(2019 Main, 10 Jan I)
(a) 11
(b) 10
(c) 12
(d) 18
Show Answer
Solution:
- Let $f(x)=(c-5) x^{2}-2 c x+(c-4)=0$.
Then, according to problem, the graph of 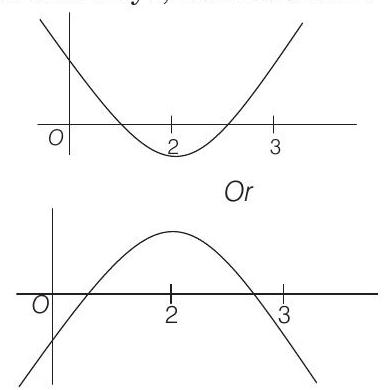$y=f(x)$ will be either of the two ways, shown below.
In both cases $f(0) . f(2)<0$ and $f(2) f(3)<0$
Now, consider
$$ f(0) f(2)<0 $$
$\Rightarrow \quad(c-4)[4(c-5)-4 c+(c-4)]<0$
$\Rightarrow \quad(c-4)(c-24)<0$
$\Rightarrow \quad c \in(4,24)$
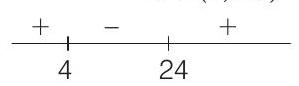
Similarly, $f(2) \cdot f(3)<0$
$\Rightarrow[4(c-5)-4 c+(c-4)]$
$$ \begin{aligned} & {[9(c-5)-6 c+(c-4)]<0} \\ & \Rightarrow \quad(c-24)(4 c-49)<0 \\ & \begin{array}{lll}
- & - & + \\ \hline 49 / 4 & 24 \end{array} \\ & \Rightarrow \quad c \in \frac{49}{4}, 24 \end{aligned} $$
From Eqs. (i) and (ii), we get
$$ c \in \frac{49}{4}, 24 $$
$\therefore$ Integral values of $c$ are 13,14 , 23. Thus, 11 integral values of $c$ are possible.
