Theory of Equations 4 Question 1
1. Let
(2019 Main, 12 Jan I)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 1. (d)
Solution:
- Given parabola is
Since,
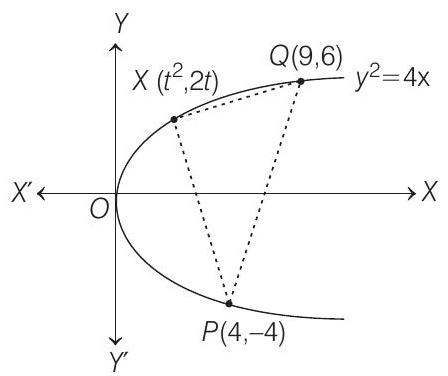
Now, as
The maximum area (in square units)






