Straight Line and Pair of Straight Lines 2 Question 8
8. Lines $L _1 \equiv a x+b y+c=0$ and $L _2 \equiv l x+m y+n=0$ intersect at the point $P$ and makes an angle $\theta$ with each other. Find the equation of a line $L$ different from $L _2$ which passes through $P$ and makes the same angle $\theta$ with $L _1 \cdot y$
$(1988,5 M)$
Show Answer
Answer:
Correct Answer: 8. $2(a l+b m)(a x+b y+c)-\left(a^{2}+b^{2}\right)(l x+m y+n)=0$
Solution:
- Since, the required line $L$ passes through the intersection of $L _1=0$ and $L _2=0$.
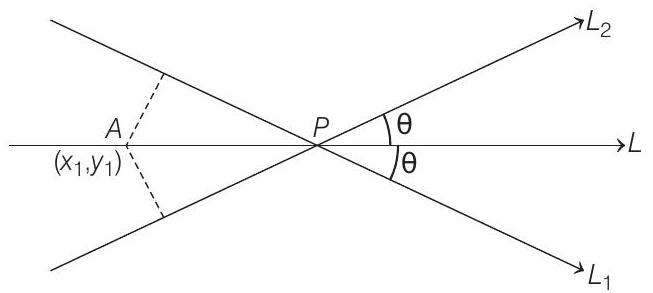
So, the equation of the required line $L$ is
$$ L _1+\lambda L _2=0 $$
i.e. $(a x+b y+c)+\lambda(l x+m y+n)=0$
where, $\lambda$ is a parameter.
Since, $L _1$ is the angle bisector of $L=0$ and $L _2=0$.
$\therefore$ Any point $A\left(x _1, y _1\right)$ on $L _1$ is equidistant from $L _1=0$ and $L _2=0$.
$$ \begin{aligned} & \Rightarrow \quad \frac{\left|l x _1+m y _1+n\right|}{\sqrt{l^{2}+m^{2}}} \\ &=\frac{\left|\left(a x _1+b y _1+c\right)+\lambda\left(l x _1+m y _1+n\right)\right|}{\sqrt{(a+\lambda l)^{2}+(b+\lambda m)^{2}}} \end{aligned} $$
But, $A\left(x _1, y _1\right)$ lies on $L _1$. So, it must satisfy the equation of $L _1$, ie, $a x _1+b y _1+c _1=0$.
On substituting $a x _1+b y _1+c=0$ in Eq. (ii), we get
$$ \begin{array}{rlrl} & & \frac{\left|l x _1+m y _1+n\right|}{\sqrt{l^{2}+m^{2}}} & =\frac{\left|0+\lambda\left(l x _1+m y _1+n\right)\right|}{\sqrt{(a+\lambda l)^{2}+(b+\lambda m)^{2}}} \\ \Rightarrow & \lambda^{2}\left(l^{2}+m^{2}\right) & =(a+\lambda l)^{2}+(b+\lambda m)^{2} \\ \therefore & \lambda & =-\frac{\left(a^{2}+b^{2}\right)}{2(a l+b m)} \end{array} $$
On substituting the value of $\lambda$ in Eq. (i), we get
$$ (a x+b y+c)-\frac{\left(a^{2}+b^{2}\right)}{2(a l+b m)}(l x+m y+n)=0 $$
$\Rightarrow 2(a l+b m)(a x+b y+c)-\left(a^{2}+b^{2}\right)(l x+m y+n)=0$
which is the required equation of line $L$.
