Straight Line and Pair of Straight Lines 1 Question 70
70. For a point
(2014 Adv.)
Show Answer
Solution:
- PLAN Distance of a point
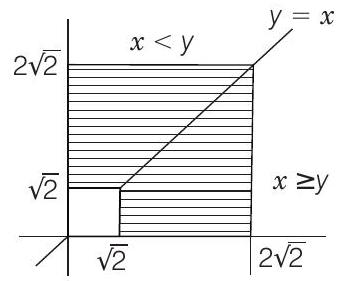
Let
Now,
Case I
Case II






