Straight Line and Pair of Straight Lines 1 Question 63
63. Two sides of a rhombus
Show Answer
Solution:
- Let the coordinates of
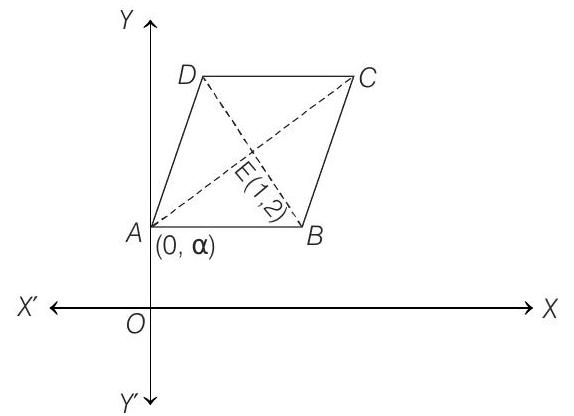
Thus, the diagonals of the rhombus are parallel to the lines
Hence, the coordinates are






