Straight Line and Pair of Straight Lines 1 Question 63
63. Two sides of a rhombus $A B C D$ are parallel to the lines $y=x+2$ and $y=7 x+3$. If the diagonals of the rhombus intersect at the point $(1,2)$ and the vertex $A$ is on the $Y$-axis, find possible coordinates of $A$.
$(1985,5 M)$
Show Answer
Solution:
- Let the coordinates of $A$ be $(0, \alpha)$. Since, the sides $A B$ and $A D$ are parallel to the lines $y=x+2$ and $y=7 x+3$, respectively.
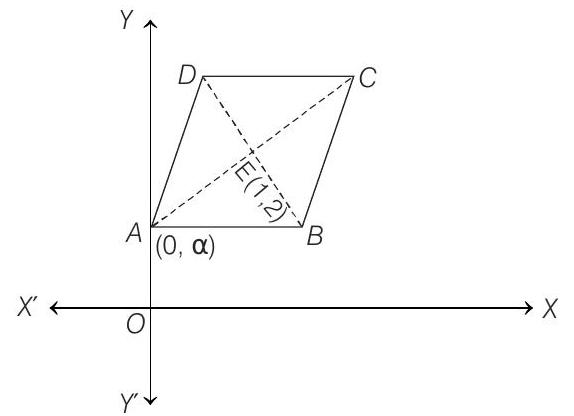
$\therefore$ The diagonal $A C$ is parallel to the bisector of the angle between these two lines. The equation of the bisectors are given by
$$ \begin{aligned} & \frac{x-y+2}{\sqrt{2}} & = \pm \frac{7 x-y+3}{\sqrt{50}} \\ \Rightarrow & 5(x-y+2) & = \pm(7 x-y+3) \\ \Rightarrow & 2 x+4 y-7=0 & \text { and } 12 x-6 y+13=0 . \end{aligned} $$
Thus, the diagonals of the rhombus are parallel to the lines $2 x+4 y-7=0$ and $12 x-6 y+13=0$.
$$ \begin{array}{rlrlrl} & & & \text { Slope of } A E & =-\frac{2}{4} \quad \text { or } & \frac{12}{6} \\ & \Rightarrow & \frac{2-\alpha}{1-0} & =-\frac{1}{2} \quad \text { or } & \frac{2-\alpha}{1-0}=2 \\ & \Rightarrow & \alpha & =\frac{5}{2} \quad \text { or } & \alpha=0 . \end{array} $$
Hence, the coordinates are $(0,5 / 2)$ or $(0,0)$.






